|
jämför areorna |
Svar: De tre areorna
är lika stora.
Lösning:
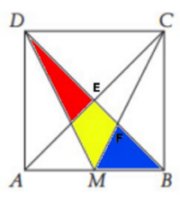
Kalla skärningspunkten mellan diagonalerna för E,
skärningspunkten mellan BD och CM för F och kvadratens sida för
a.
Triangeln MBF är likformig med triangeln CDE. Alla
sträckor i triangeln CDE är dubbelt så stora som sträckorna i
triangeln MBF.
Den blå triangeln
Basen är a/2 och höjden
a/3 (enligt likformighet)
Area: a/2 . a/3 . 1/2 = a2/12
a.e. |
 |
|
Den gula fyrhörningen
Arean = arean av ABE - 2 gånger arean av triangeln MBF =
a2/4 - 2a2/12 = 3a2/12 - 2a2/12
=a2/12 a.e.
Den röda triangeln
Arean = arean av triangeln MBD - arean av den blå triangeln
- arean av den gula fyrhörningen =
a/2 . a . 1/2 - a2/12
- a2/12 =
a2/4 - a2/12 - a2/12 = a2/12
a.e.
|
|
talet c |
Svar: Talet c = 4
Lösning:
Permuteringen ger talen abc, acb, bac, bca, cab, cba
Värdet av talet abc är 100a + 10 b + c
Värdet av alla sex talen blir efter förenkling
222(a + b + c) = 1554
a + b + c = 7
Villkoren att talen är naturliga tal och att a <
b < c medför att c måste vara 4
|
|
kast med mynT |
|
Svar: 27/64
Lösning:
Lukas kast med tre mynt har 8 möjliga utfall, vart och
ett med sannolikheten 1/8 om man tar hänsyn till ordningen.
Jag förkortar sannolikhet som p (eng. probability)
1)
Lukas får 3 kronor: Amanda får inget mynt att kasta
2) Lukas får 2 kronor (p = 3/8, eftersom det finns tre
möjligheter att få 2 kronor:
krona_krona_klave, krona_klave_krona, klave_krona_krona):
Amanda kastar 1 mynt (p för
1 krona = 1/2)
3/8
·
1/2 = 3/16
3) Lukas får 1 krona (p = 3/8): Amanda kastar 2 mynt (p för
1 krona = 1/2)
3/8
·
1/2 = 3/16
4) Lukas får 0 krona (p = 1/8): Amanda kastar 3 mynt (p för
1 krona = 3/8)
1/8
·
3/8 = 3/64
Sannolikheten för att Amanda får exakt en krona är 3/16 +
3/16 + 3/64 = 27/64
Euklides 12 2010
|
|
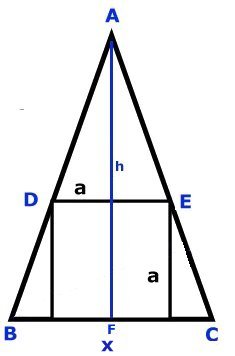
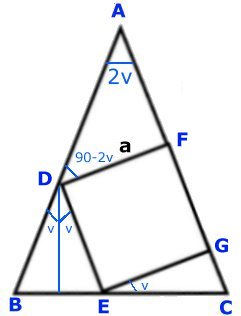
Den likbenta triangeln |
a)
Svar:
Förhållandet BC:AF = 1:1
Lösning:
Antag att BC är x (l.e.)
Triangeln ADE är likformig med triangeln ABC.
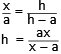
Arean av triangeln ABC
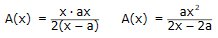
Derivera!
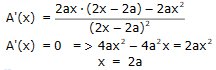
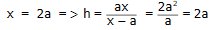
Förhållandet BC:AF = 2a:2a =1:1
|
 |
b)
Svar:
Förhållandet BC:AF = 2:1
Lösning:
Antag att AC är x (l.e.)
Triangeln BDE är likformig med triangeln BAC.
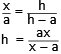
Arean av triangeln ABC
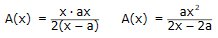
Derivera!
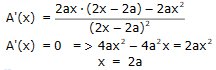
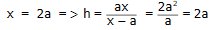
Med hjälp av derivering ovan fick vi fram att sidan AC
(och sidan AB) är lika lång som höjden mot sidan AC.
Studera triangeln ABG. Höjden BG kan endast vara lika lång
som sidan AB, om höjden BG sammanfaller med sidan AB.
Då är vinkeln BAC rät och triangeln ser ut som i figuren
till höger.
Av figuren framgår det att BC:AF = 2:1
Staffan R. har föreslagit den här lösningen:

|
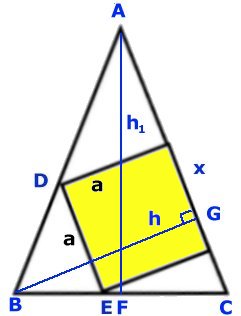
Så här ser det ut i verkligheten
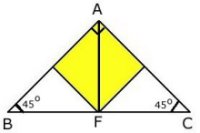
Triangeln är en 45, 45, 90 graders triangel!
|