Svar: 2018
Lösning:
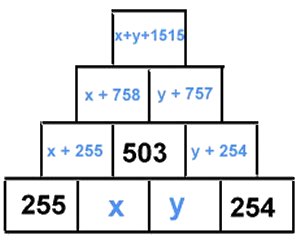
Vi kallar talen i de två tomma rutorna i nedersta raden för
x och y.
När vi fyller i rutorna enligt den givna instruktionen, blir
talet i den översta rutan
x + y + 1515
Enligt de två nedersta raderna är x + y = 503
Talet i den översta rutan är därför 503 + 1515 = 2018.
|
 |
|
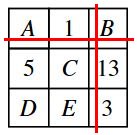
Den magiska kvadraten |
Svar: A = 15, B = 11, C =
9, D = 7 och E = 17
Lösning:
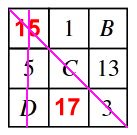
Om man jämför de rödmarkerade rutorna, inser
man att
A = 15
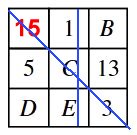
Om man jämför de
blåmarkerade rutorna, inser man att
E = 17 Om man jämför de
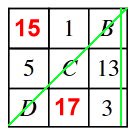
grönmarkerade rutorna, inser man att
C + D = 16 (1)
Om man jämför de
lilamarkerade rutorna, inser man att
C = D + 2 (2)
Ekvationssystemet av (1) och (2) ger C = 9 och D = 7
Sedan är det lätt att räkna ut att
B = 11 |
|
|
|
parallelltrapetset |
Svar:
50 cm2
Lösning:
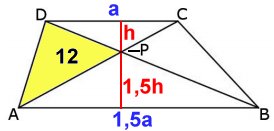
Antag att CD är a cm. Då är sidan AB 1,5 a
cm (50 % längre).
Trianglarna ABP och CDP är likformiga. Därför
förhåller sig höjderna som baserna, dvs. om
höjden i triangeln CDP är h cm, är höjden i
triangeln ABP 1,5h cm. |
 |
Arean av triangeln ACD - arean av triangeln CDP
= arean av triangeln ADP.
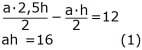
Arean av
parallelltrapetset är
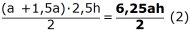
men ah = 16 (ekv. 1)
Därför blir arean av parallelltrapetset
6,25 . 16/2 = 50 (cm2)
|
|
de
gröna månskärorna |
Svar: Den sammanlagda arean
av
de gröna områdena är 6 cm2.
Lösning:
Beteckningar för sidorna AB, AC och BC framgår av figuren.
Vinkeln C är randvinkel på en halvcirkelbåge i den
största cirkeln. Vinkeln C är därför 90o.
Enligt Pytagoras sats på den rätvinkliga triangeln ABC
får vi
a2 + b2 = c2 som kan
skrivas
a2 + b2 - c2
= 0
(1) |
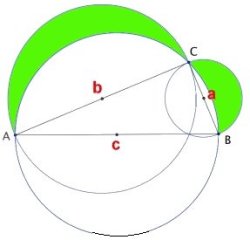 |
För att beräkna arean av de gröna områdena gör vi så här:
1)
Summera areorna av halvcirklarna på diametrarna AC och
BC.
2) Subtrahera arean av halvcirkeln på diametern AB.
3)
Lägg till arean av triangeln ABC.
Enligt texten i uppgiften är arean av triangeln ABC 6 cm2
a2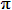 /2
+ b2 /2
+ b2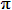 /2
- c2 /2
- c2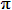 /2
+ 6 cm2 = /2
+ 6 cm2 =
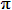 /2(a2
+ b2 - c2) + 6 cm2
=
6 cm2, eftersom a2 + b2 - c2
= 0 enl. ekv. (1) /2(a2
+ b2 - c2) + 6 cm2
=
6 cm2, eftersom a2 + b2 - c2
= 0 enl. ekv. (1)
Alltså är arean av de gröna områdena lika stor som arean
av triangeln ABC. |
|
|