|
Uppgift 1: Ta ett tal
| Lösning: |
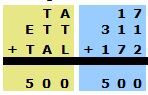 |
Vi undersöker först om
summan A + T + L
i entalskolumnen kan vara 10. I så fall är summan
i tiotalskolumnen 2T + A + 1 (=
minnessiffra). Denna är också lika med 10,
eftersom T enligt hundratalskolumnen är ≤3.
En jämförelse mellan entals- och tiotalskolumnen ger ekv.:
A + T + L =
2T + A + 1 dvs. L = T + 1
I hundratalskolumnen måste de två siffrorna vara 1 och 3.
Fall 1: Talet E = 1 och talet T = 3
Men i så fall blir också A = 10 - 1 - 2.3
= 3 enligt tiotalskolumnen.
Två olika bokstäver (T och A) får inte motsvara samma tal!
Fall 2: Talet E = 3 och talet T = 1 (och L =
2)
I så fall blir A = 7 (entalskolumnen) och vi har
hittat det rätta svaret.
Anm.: En undersökning av möjligheten att
summan i entalskolumnen är 20 ger ingen
lösning. |
|
|
Uppgift 2: Den tankspridde professorn.
Svar: Sträckan PC är 20 m och sträckan PD
19 m. |
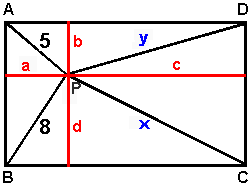
Lösning:
P:s avstånd till rektangelns
sidor är a, b, c och d (se figur).
Antag att sträckan PC är x cm och sträckan PD är y cm.
Pytagoras sats ger:
a2 + b2 = 52
a2 + d2 = 82
c2 + d2 = x2
b2 + c2 = y2
|
 |
Efter förenkling får man x2 - y2 =
39, dvs. (x + y)(x - y) =39
Denna ekvation ger två lösningar:
Alt. 1: x + y = 39
x - y = 1
Svar: x = 20 och y = 19
Alt. 2: x + y = 13
x - y = 3
Svar: x = 8 och y = 5
(Denna lösningen duger inte, eftersom
avståndet
från punkten P till aulans fyra hörn är fyra olika naturliga tal.)
Slutsats när sträckorna PA, PB, PC och PD är fyra olika naturliga tal:
|
1. |
Det ena av
sträckorna PA och PB måste vara ett jämnt tal och det andra ett
udda tal. |
|
2. |
Om sträckan PA
< sträckan PB, gäller följande samband:
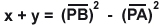 |
(1) |
|
x = y + 1
|
(2) |
|
|
|