Julpyssel (lösningar)

Tomteluvan

Lösning: Violett Tomteluvan byter färg enligt regnbågens färger (rött, orange, gult, grönt, blått, indigo och violett).

Jultomten
Jultomten säger:
HUR SKA JAG HINNA UT TILL ALLA BARNEN NÄR RUDOLF FORTFARANDE SAKNAR BLÅLJUS?  
Caesarkryptot, där alla bokstäver förskjutits 13 steg.
OBS! Tomten som gick i skolan för länge sedan, använder det svenska alfabetet med 28 bokstäver, dvs. ett alfabet utan w.

Knäckformarna

Svar: 5 knäckformar. Ett par tänkbara varianter framgår av fig. nedan.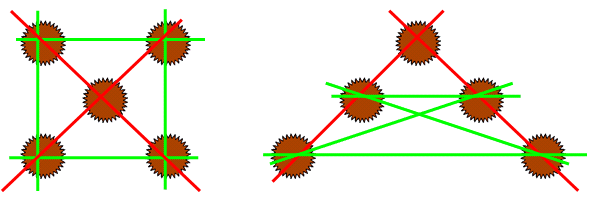

Jultomten

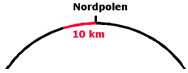
Svar: Avståndet från tomtens hus till Nordpolen är mindre än 10 km. Ex.: Tomten bor 8 km från Nordpolen. Han startar i riktning norrut. Efter 8 km har han nått Nordpolen. Han fortsätter ytterligare 2 km utan att ändra riktning men nu går han ju söderut. Efter middagspausen går han i riktning norrut. Efter 2 km har han nått Nordpolen och efter ytterligare 8 km är han hemma igen!

Önskelistorna

Fönsterrutan

Fredrik är den skyldige! Lösning: Om Anton ljuger, talar även David osanning. Om Calle ljuger, talar även David och Fredrik osanning. Om David ljuger, talar Fredrik osanning. Om Fredrik ljuger, talar de andra sanning.

Registreringsnumret

Svar: TOK 865 Lösning: Enklaste formen av kodning är väl att ersätta A med 1, B med 2 osv. Då blir K = 11. Registreringsnumret skulle i så fall (efter kodning) sluta med 11, 8, 6, 5 : Talen bildar en serie! Vi undersöker därför hur de två första talen i serien skulle se ut och finner att de måste vara 20 resp. 15. Motsvarande bokstäver blir T och O.

Tomtesäcken I

Säcken skall rymma 810 liter. (Tomtenissarna är 9, 9 och 10 år gamla.) Kommentar: Det här problemet kan nog duktiga låg- och mellanstadieelever lösa: Med hjälp av miniräknare kan man lätt testa olika värden och konstatera, att tomtenissarna bör vara så nära varandra i ålder som möjligt. Matematiskt kan man visa det genom derivering: 1) Antag, att tomtenissarna är x, y och (28-x-y) år 2) Tomtesäckens volym blir då xy(28-x-y)= 28xy-x2y-xy2  3) Derivering med avseende på x ger 28y-2xy-y2 4) Derivering med avseende på y ger 28x-x2-2xy 5) Sätt derivatorna lika med noll. 6) Efter förenkling får man  28-2x-y=0 och 28-x-2y=0 7) Bilda ett ekvationssystem av dessa ekvationer. 8) Lösningen till ekvationssystemet blir att alla tre tomtenissarna är 9 1/3 år. Eftersom alla fyller år den dagen duger bara heltalslösningar. Åldrarna 9, 9 och 10 år ger maximal storlek på säcken.

Julklappspaketet  Svar: Julklappen har följande mått:  a = 72 cm   b = 96 cm   c = 90 cm Lösning: Snörets längd är 2a + 2b +4c + 100 (cm) Antag att a = 12x cm     b = 16x cm    c = 15x cm Ekv.: 2 . 12x + 2 . 16x + 4 . 15x + 100 = 796 116 x = 696      x = 6 Lådans mått: a = 12x = 72 cm b = 16x = 96 cm c = 15x = 90 cm

Önskelistorna 2 Svar: 14 400 önskelistor. Lösning: * När de två första siffrorna kastades om, ökades antalet med 27000.  Det måste innebära att antalet önskelistor ligger i intervallet 10000 - 100000 samt att skillnaden mellan de två första siffrorna är 3. Det kan man lätt inse genom att testa några olika några exempel eller genom att ställa upp en ekvation. Antag att tiotusentalssiffran är x och tusentalssiffran y i talet som anger antalet önskelistor. Ekvation: 10y + x - 10x - y = 27 9y - 9 x = 27 y - x = 3 * Antalet önskelistor är lika med summan av kvadraten och kuben på ett visst tal (z). z2 + z3 = z3 + z2 = z2(z + 1) * Antalet önskelistor är en jämn kvadrat. Då måste också (z + 1) vara en jämn kvadrat. Vi testar:  15.15.16 = 3600  För litet! 24.24.25 = 14400 Ligger i rätt intervall och uppfyller övriga villkor! 35.35.36 = 44100  De två första siffrorna uppfyller inte villkoret! 48.48.49 =112896    För stort! Anm.:  Man kan också ta fram lösningen med ett enkelt BASIC-program. 10 FOR X= 1 TO 100 20 LET S= X^3+X^2 30 IF SQR(S)= INT(SQR(S)) THEN PRINT X;S 40 NEXT X

Stavgång

Rudolf med röda mulen

Tomtesäcken II

Svar: I tomtens säck fanns det 93 st 7 l-paket, 2 st 13 l-paket och 5 st 20 l-paket. Lösning: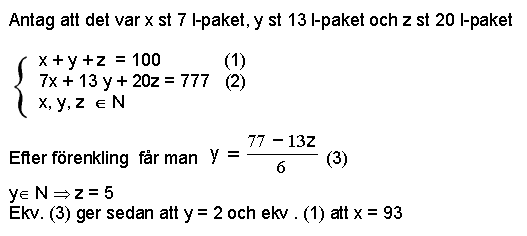

Tomtenissarna

Svar: 12 tomtenissar Lösning: Det gäller att leta bland primtalstvillingarna under 50. Man kan lätt dra följande slutsatser: 1) Antalet tomtenissar måste vara ett jämnt tal (eftersom två primtal är närmsta grannar). 2) Om kvadrattalet faktoriseras, måste varje faktor förekomma minst två gånger. Därför är kvadrattalet  säkert delbart med 4. Kvadrattalet är också delbart med 9, eftersom det är lika med summan av de tre talen. Endast talet 36 uppfyller det villkoret. Antalet tomtenissar är därför 12 st (och primtalstvillingarna är 11 och 13).

Den borttappade siffran Svar: Den borttappade siffran är 3. Lösning: Alla tal i nians tabell har en siffersumma som är jämnt delbar med nio. Ex.: 9, 18, 27, 36, ..... 747, 756, ........ 7983, 7992 ..... Om vi kan bevisa att svaret är ett tal i nians tabell så kan vi lätt räkna ut vilken siffra, som saknas! Antag att det fyrsiffriga talet har siffrorna a, b, c och d. Talets värde är då 1000*a+100*b+10*c+d. Vi visar vad som händer om siffrorna efter omkastningen kom i följande ordningsföljd: cdba. (Pröva gärna en annan ordningsföljd för att se att resultatet blir det samma.) Det nya talets värde är då 1000*c+100*d+10*b+a. Differensen blir då 1000*a+100*b+10*c+d - (1000*c+100*d+10*b+a) Efter förenkling får man 999a+90b-990c-99d, vilket också kan skrivas 9 (111a+10b-110c-11d) V.S.B. Siffersumman av de tre kända siffrorna är 2+5+8 = 15. Närmast högre heltal, som är jämnt delbart med 9 är 18. 18-15 = 3 Anm.: En mera allmängiltig lösning skulle kunna se ut så här: Värdet av siffran a i det ursprungliga talet är a*10n och i talet med siffrorna omkastade a*10m Fall 1: (n>m) Differensen blir då a(10n - 10m) = a*10m(10n-m - 1). Om vi beräknar värdet av parentesen, kommer vi att få ett tal som består av enbart nior oberoende av vilket värde exponenten (n-m) har. Parentesen är därför delbar med 9. Fall 2: (n<m) Differensen blir då a(10n - 10m) = -a(10m - 10n) = -a*10n(10m-n - 1) där parentesen är delbar med 9.

Avlöningen Se månadens problem (jan 2007)

Nötskålen

Svar: 32 paranötter, 64 valnötter och 128 hasselnötter.  Lösning:  Antag att det fanns x paranötter, ax valnötter och a2x hasselnötter På juldagen fanns det x paranötter, ax/4 valnötter och (a2x - 120) hasselnötter. Upplysningarna ovan ger följande geometriska serie:  a2x -120, ax/4 , x , ax, a2x  Ekv. 1: a2 .ax/4 = ax  dvs. a = 2 Ekv. 2: a2(a2x -120) = x  Insättning av a = 2  ger 4(4x -120) = x  x = 32

Ljusstaken