|
Serietabellen |
Svar:
5 matcher slutade oavgjort.
Lösning:
Varje lag spelar 4 matcher mot 3
lag: 4 . 3 matcher = 12
matcher
Totalt för 4 lag: 4 .
12/2 matcher = 24 matcher
(Division med 2 är
nödvändig. Annars räknas varje match 2 gånger).
Om
varje match slutat med seger för ett av lagen hade den
sammanlagda poängsumman blivit 24 .
3 poäng = 72 poäng
I turneringen blev
den sammanlagda poängsumman 22 + 19 + 14 + 12 = 67
poäng.
Vid seger delas det ut 3 poäng och vid
oavgjort 1 + 1 = 2 poäng.
Sammanlagda poängsumman
minskar alltså med en poäng för för varje oavgjord
match. 72 - 67 = 5, dvs. 5 matcher slutade oavgjort.
|
|
|
|
|
beviset |
Bevis:
Triangeln BDE är likformig med
triangeln BCA.
AC = d1
BD = d2
DE = a
Likformighet ger
DE/CA = BF/BO
|
 |
|
|
rutorna |
Svar:

Lösning:
Antagande:
Talen i fjärde och femte rutan är a resp. b
|
|
|
|
11 |
|
|
|
|
14 |
|
6 |
a |
b |
6+a+b |
6+2a+2b |
12+3a+4b |
24+6a+7b |
42+11a+13b |
78+20a+24b |
Det ger ekvationssystemet
6 + a + b = 11
78 + 20a + 24b
= 14
Det ger lösningen a = 46 och b = - 41
Insättning av
värdena för a och b ger heltalen i rutorna 4-12.
Antagande:
Talen i första och andra rutan är c resp. d
Det ger
ekvationssystemet
c + d + 6 = 46
d + 6 + 46 = - 41
Det
ger lösningen c = 133 och d = - 93
|
|
DE
TRE SISTA SIFFRORNA |
Svar: De
tre sista siffrorna är 234 eller 517
Anm.: Hur många
lösningar är det till uppgiften:
Vilka
är de tre sista siffrorna i detta
tal med 2023 siffror?
Lösning:
Tvåsiffriga tal delbara med 17
är 17, 34, 51,
68 och 85
Tvåsiffriga tal delbara med 23 är
23, 46,
69 och 92
För
att de tvåsiffriga talen ska vara
delbara med 17 eller 23 måste de tre
första siffrorna i talet med 2022
siffror vara 346.
Den
fjärde siffran kan vara 8 eller 9,
eftersom 68 är delbart med 17 och 69
med 23.
Fall 1: Fjärde
siffran är 8
Då måste
femte siffran vara 5 (talet 85 är
delbart med 17), sjätte siffran vara
1 (51 är delbart med 17) och sjunde
siffran 7 (17 är delbart med 17).
Men här tar det stopp! Inget
tvåsiffrigt tal som börjar med
siffran 7 är delbart med 17 eller
23.
Slutsats: Fjärde siffran kan
inte vara 8, om mönstret ska
upprepas.
Fall 2: Fjärde
siffran är 9
Då måste
femte siffran vara 2 (talet 92 är
delbart med 23), sjätte siffran vara
3 (23 är delbart med 23), sjunde
siffran 4 (34 är delbart med 17),
åttonde siffran 6 (46 är delbart med
23), nionde siffran 9
(69 är
delbart med 23) och tionde siffran 2
(talet 92 är delbart med 23).
Vi
ser då ett mönster: siffrorna 34692
upprepas.
|
Siffra nr |
2016 |
2017 |
2018 |
2019 |
2020 |
2021 |
2022 |
|
|
3 |
4 |
6 |
9 |
2 |
3 |
4 |
Men vi får också en lösning från
fall 1!
|
Siffra nr |
2016 |
2017 |
2018 |
2019 |
2020 |
2021 |
2022 |
|
|
3 |
4 |
6 |
8 |
5 |
1 |
7 |
|
|
|
|
rektangeln |
Svar:
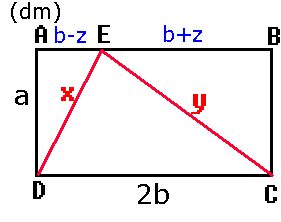
Punkten ligger 1 dm från ena hörnet på sidan AB.
Lösning:
Givet:
x . y = 10
Längdenhet: dm
Sökt:
Sträckan AE.
Allmän lösning:
Sidan AD = a, sidan AB = 2b,
sträckan AE = b - z och
sträckan EB = b + z
Pytagoras sats ger:
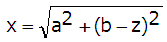
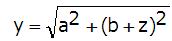
Efter förenkling får vi att
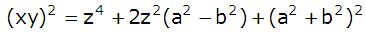 (1)
(1)
Dessutom vet vi att
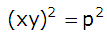 (I vårt exempel är p = 10)
(2)
(I vårt exempel är p = 10)
(2)
Ledvis subtraktion (1) - (2) ger
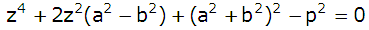
Lös ekv. med avseende på z2

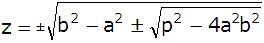
Specialfallet i den här uppgiften:
a = 2, b = 2,5 och p = 10 ger
z = ±
1,5
Fall 1: b - z = 2,5 - 1,5 = 1 och b + z = 2,5 + 1,5 = 4
Fall 2: b - z = 2,5 - (-1,5) = 4 och b
+ z = 2,5 +(-1,5) = 1
Författaren till denna
uppgift har valt en rektangel där punkten E:s läge på sida
AB medför att trianglarna ADE och BCE är likformiga. Då kan
man lätt visa att även triangeln AEB är rätvinklig och
likformig med trianglarna ADE och BCE.
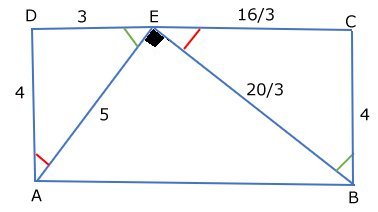
Ett exempel på hur man hittar en
rektangel,
där såväl rektangelns sidor
som sammanbindningslinjerna är naturliga tal:
| * |
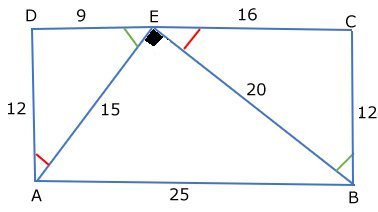
Utgå från den rätvinkliga triangeln ADE med sidorna 3, 4
och 5. |
|
* |
Anpassa sidan AB så att vinkeln AEB blir rät. |
|
* |
Då är trianglarna ADE och BCE likformiga. |
|
* |
Likformighet ger att
CE = 16/3 och BE = 20/3. |
|
* |
Om man förstorar figuren i skala 3:1 blir sidorna AB och
BC 25 och 12 samt sträckorna AE och BE 15 och 20. |
|
 |
|
|
|
|
|
|