|
Den indiske vishetsläraren |
Svar:
a) 1,414215...
b) Närmevärde till kvadratroten ur två
c) Med fem decimalers noggrannhet
(Korrekt närmevärde är
1,414213...)
Lösning:
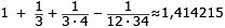
Anm.: I Indien kunde man beräkna närmevärden till
kvadratrötter på 500-talet f. Kr.
|
|
|
Flytta en siffra del1 |
26
- 63 = 1
Lösning:
Flytta
6:an så att den blir en exponent!
26 -
63 = 1
|
|
Flytta en siffra del2 |
24
- 7 = 51
Lösning:
Flytta
1:an till vänstra ledet.
24 -
17 =
5
(Talsystemets bas måste vara
större är
7, eftersom siffran 7 finns med.
Svaret 5 visar att talsystemets
bas måste vara mindre än 10.
Med 10 som bas är ju 24 - 17 = 7).
Talsystemets bas måste då vara 8
eller 9.
Man kan testa vilken bas som är den
rätta eller sätta upp en
ekvation, där x är talsystemets bas.
24 -
17 = 5
2x + 4 - (x + 7) = 5
x - 3 = 5
x = 8
Talen är skrivna i det oktala
talsystemet.
248 -
178 = 58 Kontroll:
248 = 2010,
178
= 1510
och
58 =
510
2010
- 1510 = 510
|
|
månghörningen |
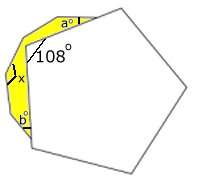
Svar: Det är
en regelbunden niohörning.
Lösning:
Vinkelsumman i en månghörning
med n hörn är
(n - 2) . 180o
Vinkelsumman i femhörningen är (5 -
2) . 180 = 540
Varje vinkel i femhörningen är 540/5
o = 108o
Antag att varje vinkel i den delvis
täckta månghörningen är x o
Vinkelsumman i den gula sjuhörningen
ger ekvationen
4x + 88 + (360 - 108) = (7 - 2)
. 180
x = 140
Antag att den delvis täckta
månghörningen har n hörn.
Ekv.: n . 140 = (n
- 2) . 180
40n = 360
n = 9
|
 |
|
siffersumman |
Svar: Siffersumman är alltid 9 eller 18.
Bevis:
Antag att det ursprungliga tresiffriga talet är xyz.
Talets värde är då 100x + 10y + z
Differensen av talet och dess siffersumma är
100x + 10y + z - (x + y + z) =
99x + 9y = 9(11x + y).
Enligt en välkänd räkneregel är siffersumman delbar med 9, om
talet är delbart med 9.
Talet 9(11x + y) är jämnt delbart med 9.
Siffersumman i differensen 9(11x + y) är 9 eller 18. (Siffersumman 27 skulle
innebära att differensen är 999, vilket naturligtvis är orimligt.)
|
|
|
|
BEVISET |
|
|
|