|
primtalen |
a)
Svar: 1/15
Lösning:
Två primtal kan väljas bland tio
primtal enligt
formeln
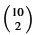 = 45 = 45
Summan kan bli 24 på 3 olika sätt: 5
+ 19, 7 + 17, 11 +13
Sannolikhet: 3/45 = 1/15
b)
Svar: 1/5
Lösning:
Om det ena primtalet är 3, är
produkten av två primtal jämnt
delbar med 3.
Det kan bildas 45 par av primtal
enligt formeln
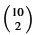 = 45. = 45.
Det ena primtalet är alltså 3. Det
andra primtalet kan då väljas på 9
sätt.
Sannolikhet: 9/45 = 1/5
|
|
hundrametersloppet |
Svar:
a) Amanda kommer först i mål. I lopp 1 är hon 5 m före Sara
i mål.
I nästa lopp springer de en längre sträcka. Det gynnar Amanda
som har den
högre hastigheten. Skillnaden i löpsträcka blir därför större än 5 m, dvs.
Amanda
vinner.
b)
Svar: 0,25 m
Lösning:
Lopp 1:
När Amanda har sprungit 100 m, har Sara sprungit 95 m.
Det betyder att förhållandet mellan Saras och Amandas hastigheter är
95:100 = 19:20.
Lopp 2:
När Amanda har sprungit 100 m, har Sara sprungit 95 m, dvs. då
är de helt jämsides.
När Amanda springer återstående 5 m, springer Sara
19 .
5/20 m = 4,75 m
Avståndet mellan dem, när Amanda går i mål är 5 m - 4,75 m =
0,25 m
|
|
cylindern |
Svar:
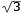
Lösning:
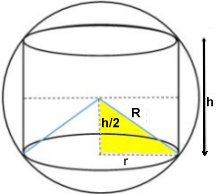
Cylinderns radie och höjd är r
resp. h
Pythagoras sats på den gula
triangeln ger
r2 + (h/2)2
= R2
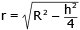 (1)
(1)
Cylinderns volym:
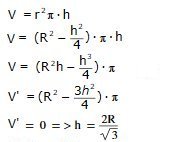
Sätt in detta värde på h i ekv. (1)
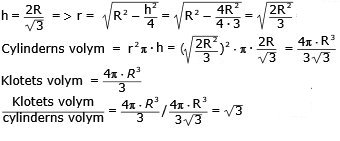
|
 |
|
summan |
Svar: 18
Lösning:
ab + cd = 38 (1)
ac + bd = 34 (2)
ad + bc = 43 (3)
Addera (2) och (3) ledvis
ac + bd + ad + bc = 34 + 43
a(c + d) + b(c + d) = 77
(a + b)(c + d) = 77
Faktorn (a + b) eller faktorn (c + d) kan inte vara lika med 1.
Då måste den ena faktorn var 7 och den andra 11. (7 * 11 = 77)
Då är a + b + c + d = 7 + 11 = 18
Anm.:
| 2 |
5 |
7 |
4 |
a, b, c och d kan anta värden
2, 4, 5 och 7
i fyra olika varianter.
|
| 5 |
2 |
4 |
7 |
| 4 |
7 |
5 |
2 |
| 7 |
4 |
2 |
5 |
|
|