Svar: Koden kan väljas på
13 sätt
Lösning:
| Kod |
Antal sätt med permutation |
| 1224444 |
6 |
| 1666666 |
2 |
| 2255555 |
2 |
| 3334444 |
2 |
| 7777777 |
1 |
| Summa |
13
|
|
|
fyrhörningen |
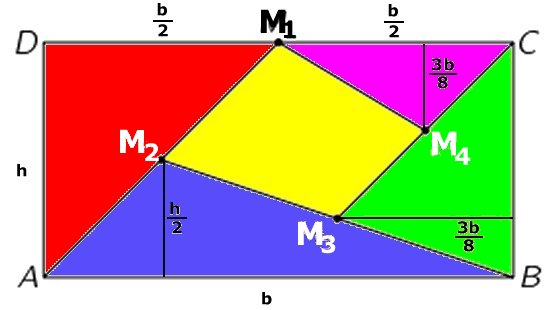 |
Svar: Fyrhörningens
area är 7/32 av rektangelns area
Lösning:
Antag att rektangelns sidor är b och h.
Höjderna i deltrianglarna beräknas med likformighet.
Exempel: Höjden i den blå triangeln är hälften av höjden i
rektangeln, eftersom M2
är mittpunkt på sträckan AM1.
Arean av den röda triangeln = arean av den blå triangeln:
bh/4
Arean av den gröna triangeln:
3bh/16
Arean av den violetta triangeln:
3bh/32
Arean av den gula fyrhörningen: bh - bh/4 - bh/4 - 3bh/16 -
3bh/32 = 7bh/32
|
|
|
kvadraten |
a)
Svar:
Kvadratens sida är
5 cm
Lösning:
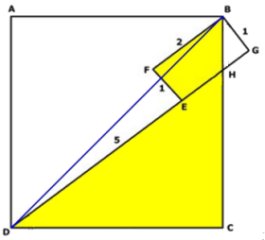
Förläng sträckan DE till punkten G, så att BFEG blir en
rektangel.
Då är BG = 1 cm och DG = 7 cm
Kvadratens diagonal BD beräknas med Pythagoras
sats på triangeln BDG.
(BD)2 = 72 + 12
(BD)2 = 50
BD =
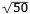 cm
cm
Kvadratens sida är
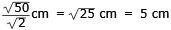
|
 |
b)
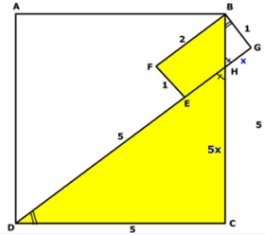
Svar: Den gula arean är 11 cm2
Lösning:
Antag att sträckan GH är
x cm.
Triangeln CDH är likformig med triangeln BGH.
Sträckan CD är 5 gånger så lång som sträckan BG.
Då är sträckan CH också
5 gånger så lång som sträckan GH, dvs. 5x cm.
Med hjälp av Pythagoras sats på triangeln BGH får vi att
sträckan BH är
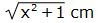 |
 |
Sträckan BC ger ekvationen

|
|
En vann, 95 försvann |
Svar: Personen sade talet 65 i den
första omgången.
Lösning:
Efter varje omgång försvinner
hälften av medlemmarna så länge det finns ett jämnt antal medlemmar kvar. Efter omgång 1 återstår 48 medlemmar, det är de
som sade tal som är kongruenta med 1 modulus 2. Efter omgång 2
återstår 24 medlemmar, de som i omgång 1 sade tal som är
kongruenta med 1 modulus 4. Efter omgång 3 återstår 12
medlemmar, de som i omgång 1 sade tal som är kongruenta med 1 modulus 8. Efter omgång 4 återstår 6 medlemmar, de som i omgång
1 sade tal som är kongruenta med 1 modulus 16. Efter omgång 5
återstår 3 medlemmar, de som i omgång 1 sade tal som är kongruenta
med 32 modulus 1, dvs. 1, 33 och 65. Därefter kommer medlemmarna
som i omgång 1 sade 33 respektive 1 att försvinna. Kvar blir den
som startade med 65.
Extrauppgift:
Svar: Den som börjar räkna i omgång 1 är säker på att vara
kvar till slut, om antalet deltagare är 2n i första omgången
(n = 1, 2 , 3...)
|