I tangentens riktning
Lätt: Svar: Radien är 7 cm. Lösning: Antag att radien är r cm. Pytagoras sats på den rätvinkliga triangeln ABO ger: r2 + 242 = (r + 18)2 r2 + 576 = r2 + 36r + 324        36r = 252           r = 7
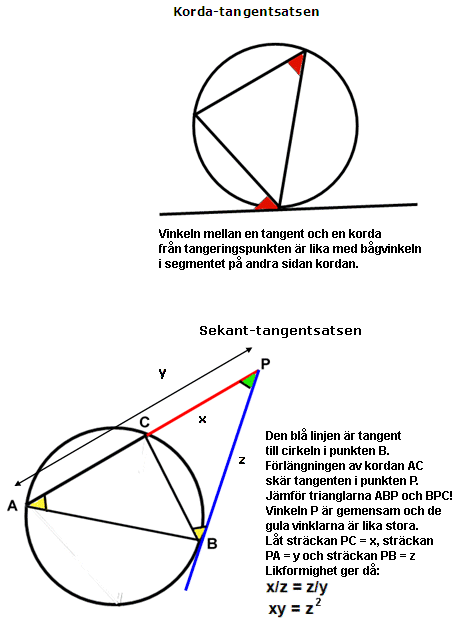
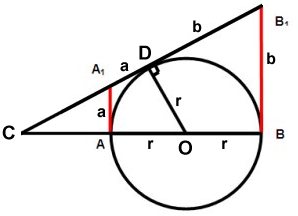
Svår: Specialfall: Om tangenten är parallell med diametern AB är sträckorna AA1 och BB1 lika långa som cirkelns radie. Det betyder att AA1 .  BB1 = r2 Därmed vet vi svaret. Nu gäller det att bevisa det också. Svar: AA1 . BB1  =  r2 Bevis: AA1 = a och BB1 = b (två tangenter från samma punkt är lika långa). Trianglarna AA1C, BB1C och DOC är likformiga (Likvinkliga trianglar) Likformighet ger a/r = AC/CD b/r = BC/CD Multiplicera ledvis! ab/r2 = AC .  BC/(CD)2 Men enligt korda-tangentsatsen är AC .  BC = (CD)2 Alltså är ab = r2  V.S.B.       Bevis för korda-tangentsatsen finns här