Månadens problem
finns den här gången med två olika svårighetsgrader.
Uppg. 1:
Lösning:
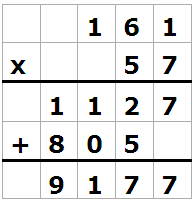
När entalssiffran i talet *** (dvs.
161) multipliceras med 7 blir svaret 7. Då är
entalssiffran i *** en etta.
7 gånger tiotalssiffran i *** ger ett svar som
slutar med en tvåa.
Då är tiotalssiffran i *** en sexa.
När *** multipliceras med 5, blir svaret
tresiffrigt. Därför kan vi dra slutsatsen att
hundratalssiffran i *** måste vara 1. |
 |
|
Uppgift 2:
Lösning:
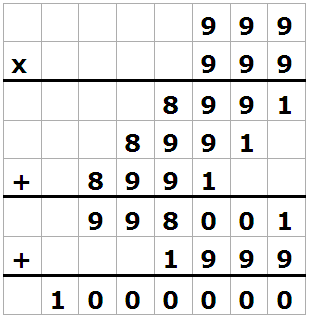
Det tal, som adderas (1***), kan vara
högst 1999.
Produkten av de tresiffriga talen måste därför vara ≥ 998001, om
slutsvaret ska bli ett sjusiffrigt tal.
Endast 999 . 999 uppfyller det villkoret.
|
 |
|
|