Jubileumsproblemet 650 000 (lösning)

Uppgift 1:

Lösningen kan se ut så här:


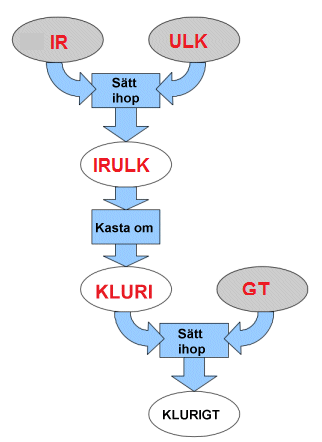
Uppgift 2:
Svar: Talen 625, 6250, 62500 och 625000 uppfyller villkoren.
Lösning:
Det finns inga ensiffriga eller tvåsiffriga tal som uppfyller villkoren.
Antag att de tal, som uppfyller villkoren är 6 ^. 10ⁿ + x       
n = 2, 3, 4, 5

   x = (6 ^. 10ⁿ + x)/25
25x = 6 ^. 10ⁿ + x
24 x = 6 ^. 10ⁿ
     x = 2,5 ^. 10^n-1

De sökta talen är 6 ^. 10ⁿ + 2,5 ^. 10^n-1
 n = 2 ger 600 + 25 = 625
 n = 3      6000 + 250 = 6250
 n = 4      60000 + 2500 = 62500
 n = 5      600000 + 25000 = 625000

Uppgift 3:
Svar: Det finns inga tal som har den egenskapen.
Lösning:
Antag att det finns ett tal, p + q, med den egenskapen.
Talet p väljs så att p består av en siffra (≠ 0) följt av ett antal nollor
(p är m ^. 10ⁿ  m = 1, 2, 3...., 9 och n är ett naturligt tal)
q = (p + q)/35
35q = p + q
34q = p
   q = p/34
Orimligt!
q = p/34 ger inte ett heltalsvärde för q.



Uppgift 4:
Svar: Pennkniven är värd 2 kr.
Lösning:
Eftersom det till slut inte finns 10 kr kvar, när det är den yngre broderns tur, måste de tillsammans ha hämtat 10 kr från försäljningssumman ett udda antal gånger.
Försäljningssumman är (antalet får)² kr
Antag att antalet får består av summan av x och ett ensiffrigt tal.
x är ett tal jämnt delbart med 10.

Det gäller då att undersöka när antalet 10-tal är udda.
Om försäljningssumman är
(x + 4)^{2 =} x² + 2x + 16   får man ett udda antal 10-tal 
(x² + 2x är ett jämnt antal 10-tal. Det finns ett udda antal 10-tal i talet 16)
(x + 6)^{2 =} x² + 2x + 36   får man ett udda antal 10-tal
(I alla övriga fall får man ett jämnt antal 10-tal.)
Det innebär den yngre brodern sista gången får 6 kr.
Om pennkniven är värd 2 kr får han sammanlagt (6 + 2) kr = 8 kr.
Den äldre brodern fick sista gången 10 kr, men sedan han givit bort sin pennkniv, blir det 10 kr - 2 kr = 8 kr.

Tillbaka