Jubileumsproblemet 300 000 (lösning)

Lätt:
Svar: Ett exempel är 550² -50²  = 302 500 - 2 500 = 300 000
Lösning:
Man inser lätt att 600 ^. 500 = 300 000
Antag att vi skriver differensen mellan två naturliga tals kvadrater som a²  - b²
Enligt konjugatregeln kan a²  - b² skrivas (a + b)(a - b)
I vårt exempel får vi 600 ^. 500 = (550 + 50)(550 - 50) = 550² -50²  = 302 500 - 2 500 = 300 000

Allmänt
Läget av (a + b) och (a - b) på tallinjen framgår av figuren nedan.


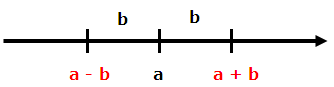
Vi kan också notera
att talet a ligger mitt emellan talen (a - b) och (a + b) (1)
att antingen är både (a - b) och (a + b) jämna tal eller är båda talen udda tal (2)

Anm.: Eftersom 300 000 kan skrivas som 2^{5 .} 3 ^. 5⁵ inser vi att båda faktorerna (a-b) och (a + b) inte kan vara udda tal.
Enligt resonemanget i punkten (2) ovan blir därför produkten 300 000, endast om båda faktorerna är jämna tal.
Mitt emellan 500 och 600 ligger talet 550.
Produkten 600 ^. 500 kan därför skrivas (550 + 50)(550 - 50)= 550² -50²

Svår:
Svar: Talet 300 000 skrivas som differensen mellan två naturliga tals kvadrater på 24 olika sätt.

Lösning:
Kvadratroten ur 300 000 är 547, 72...
Vi vet därför att det högsta värdet på (a - b) ligger något under 547, 72....
En undersökning visar att detta värde är 500.
Eftersom vi vet från den första uppgiften att (a - b) och (a + b) är jämna tal, undersöker vi vilka jämna tal, (a - b)<500, som 300 000 är jämnt delbart med.

Tillbaka