Månadens problem
januari 2022 (lösning)

Uppg. 1: 
Svar: Maja är 11 år och Niklas är 9 år.
Lösning:
Antag att Maja är x år och Niklas y år.
Majas veckopeng fördubblas: 28 < 2x + y < 32     (1)
Niklas veckopeng fördubblas: 28 < x + 2y < 32     (2)
Summera olikheterna:           56 < 3x + 3y < 64
De tal mellan 56 och 64, som är delbara med 3, är 57, 60 och 63
57/3 = 19, 60/3 = 20, 63/3 = 21

Då får vi undersöka följande fall:          
x + y = 19 x ≥ 10 2 . 10 + 9 = 29   10 + 2 . 9 = 28 Ingen lösning
x + y = 20 x ≥ 11 2 . 11 + 9 = 31   11 + 2 . 9 = 29 Lösning
x + y = 21 x ≥ 11 2 . 11 + 10 = 32 11 + 2 . 10 = 31 Ingen lösning
 
Uppg. 2:
Svar: Summan av alla positiva, tresiffriga tal som är delbara med 3 men inte
med 9 är 165 150 - 55 350 = 109 800 
Lösning:
 Summan av alla tresiffriga tal delbara med 3:
 Första tresiffriga termen delbar med 3 är 102: 3 . 34
Sista tresiffriga termen delbar med 3 är 999: 3 . 333
Antalet termer: 333 – 33 = 300 
Summa: 300(102 + 999)/2 = 165 150
 
Summan av alla tresiffriga tal delbara med 9:
 Första tresiffriga termen delbar med 9 är 108: 9 . 12
Sista tresiffriga termen delbar med 9 är 999: 9 . 111
Antalet termer: 111 – 11 = 100 
Summa: 100(108 + 999)/2 = 55 350
 

Uppg. 3:

Svar:

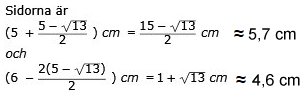
Lösning:
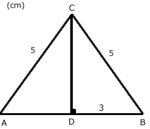
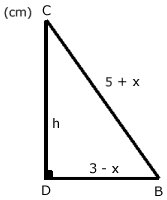
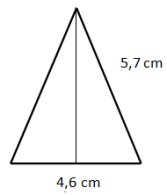
Triangeln till höger har omkretsen
(5 + 5 + 6) cm = 16 cm
Höjden CD är 4 cm (Pythagoras sats på triangeln BCD.)
Arean är b . h/2 = 6 . 4/2 cm2 = 12 cm2

Antag att den andra likbenta triangeln med samma omkrets har sidorna (5 + x, 5 + x och 6 - 2x) cm.
 -1 <  x < 3
Pythagoras sats ger:
h2 + (3 - x)2 = (5 + x)2
Efter förenkling får man

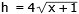
Arean ska vara 12 cm2
Ekv.:

 

 

 












 

Uppg. 4:

  
Svar: Förhållandet mellan visitkortets sidor är 20,25 : 1 ≈ 1,2 : 1
Lösning:
Om visitkortet viks längs diagonalen, så att hörnet D hamnar på bordet i punkten G, har hörnet speglats i diagonalen AC och vinkeln CED är därför rät. (fig. 2).
I det här problemet hamnar punkten D rakt ovanför punkten F på långsidan BC. Vinkeln DEF är då 45o. (fig. 1)
Låt sträckan EF = a
Sträckan DE är då
Låt sträckan CE = b

Trianglarna ADE och CEF är likformiga.
Förhållandet mellan motsvarande sträckor är (Jämför sträckorna DE och DF).

Likformighet mellan trianglarna
ADE och CDE ger:


 

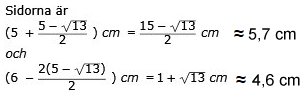Uppg. 5:
Svar: Guldmynt: 2 gram, silvermynt: 5 gram, bronsmynt: 5 gram och
         kopparmynt: 10 gram
Lösning:


 

 		 6g + 13s + 3b + 7k = 162  (1)
15g + 5s + 11b = 110       (2)
Ekv. 2: 11b måste vara delbart med 5. Då är b delbart med 5.
Enda möjligheten är att b = 5
Då kan ekvationssystemet skrivas
6g +13s + 7k = 147   (1)
15g + 5s + 55= 110   (2)   
(2) kan förenklas till s = 11 - 3g
(2) ger möjligheterna (g,s): (1,8), (2,5) eller (3,2)
(2,5) ger k = 10 i ekv. (1) Övriga alternativ ger inte heltalsvärde för k.

 

  Tillbaka