Uppg. 1:
Lösning:
 |
|
|
Uppg. 2:
Fall1:
| |
Svar: Om
Bob är snabbast, har han sprungit 30,5 varv.
Alice varvtid är 61 sekunder.
Lösning:
Båda har sprungit lika länge. Det ger ekvationen
30,5 . 60 = 30 .
t t = Alice varvtid
t = 61 |
|
Fall2: |
| |
Svar: Om
Alice är snabbast, har Bob sprungit 29,5 varv.
Alice varvtid är 59 sekunder.
Lösning:
Båda har sprungit lika länge. Det ger ekvationen
29,5 . 60 = 30 .
t t = Alice varvtid
t = 59
|
|
|
|
Uppg. 3: |
|
|
Svar:
Lösning:
Antag att sannolikheten för att få "krona" är x.
Sannolikheten för att få "krona" i båda kasten blir då x2.
Komplementhändelsen ("krona" - "klave", "klave" - "krona",
"klave" - "klave")
är 1 - x2.
Upplysningen att "krona" - "krona" är dubbelt så sannolikt som
komplementhändelsen ger ekvationen:
x2 = 2(1 - x2)
x2 = 2 - 2x2
3x2 = 2
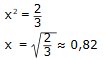 |
|
|
Uppg. 4: |
|
|
Svar: Förhållandet
mellan diamantens delar är 19:1
Lösning:
Antag att de två delarnas vikt är x och y.
Deras sammanlagda värde är 120000 kr - 11400 kr = 108600 kr
k är proportionalitetsfaktor
Innan diamanten gick sönder, gällde att k .
(vikten)2 = 120000
Vikten = x + y. Därför är k = 120000/(x + y)2
När diamanten har gått sönder, gäller
k . x2 + k . y2
= 108600
Byt ut k mot 120000/(x + y)2

|
|
|
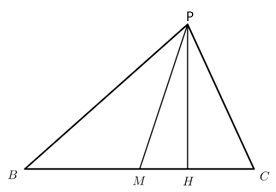
Uppg. 5:
a)
Svar:
Sträckan AP är 10 cm eller 6 cm.
Lösning: |
|
AP = x, PM =
12 - x, BP = y och CP = z
Vi börjar med att titta på triangeln BCP:
Enligt Apollonius teorem (200-talet f. Kr) för medianer
gäller att BP2
+ CP2
= 2PM2
+ BC2/2
Klicka här för att se beviset
y2 + z2
= 2
. (12 -x)2
+ 82/2
y2 + z2 = 2(12 -x)2 + 32
Addera x2 till båda leden!
x2
+
y2 + z2 = x2
+2(12 -x)2 + 32
x2 +
y2 + z2 = 3x2 - 48x + 320
Vänsterledet är summan av kvadraterna på avstånden från P
till de tre triangelhörnen.
Högerledet visar att kvadratsumman endast är beroende P:s
läge på medianen AM.
Enligt uppgiften är 3x2 - 48x + 320 = 140
x2 - 16x + 60 = 0
x1 = 10
x2 = 6
b)
Svar: Sträckan AP är 8 cm, när summan av kvadraterna på
avstånden från P till de tre triangelhörnen är så liten som
möjligt
Lösning:
f(x) = 3x2 - 48x + 320
Derivera!
f ' (x) = 6x - 48
f ' (x) = 0
 6x = 48
6x = 48
x = 8
(x = 8
 x2 +
y2 + z2 = 128)
x2 +
y2 + z2 = 128)
|
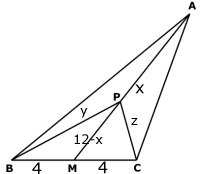
OBS!
Beträffande triangeln gäller att medianen AM = 12 cm och
sidan BC = 8 cm.
I övrigt har triangeln ett godtyckligt utseende och vi kan
inte beräkna övriga sidor eller sträckorna y respektive z. |
|
|