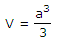Månadens problem
januari 2009 (lösning)

Problem i kubik
Månadens problem (två olika svårighetsgrader)
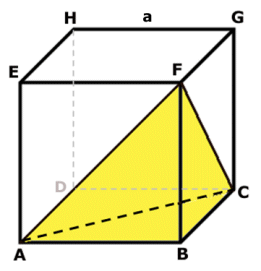
Lätt:

Svar: 1/6

Lösning:
Kubens volym är a3

Fig. ABCF är en pyramid med basytan BCF och höjden AB.
Formeln för pyramidens volym är
basytan . höjden/3.
Pyramidens volym är därför
dvs. 1/6 av kubens volym.
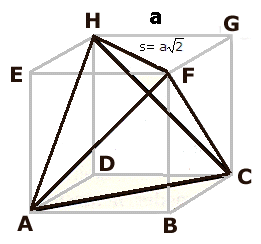
Svår:

 Svar: 1/3

Lösning:
Kubens volym är a3
Kanterna (s) i figuren ACFH
är samtliga
ACFH är alltså en tetraeder.
Volymen för en tetraeder är
Om vi sätter in s =  får vi
 
dvs. 1/3 av kubens volym.  
Man kan dock lösa problemet utan att känna till tetraederns volym genom att beräkna den del av kuben som inte hör till tetraedern.
Figuren AEHF hör inte till tetraedern.
Enligt föregående uppgift ("Lätt") är volymen av AEHF = a3/6
Det finns sammanlagt fyra sådana figurer som inte hör till tetraedern.
Tetraederns volym är därför a3 - 4a3/6 = a3/3  

 Tillbaka