Månadens problem
febuari 2024 (lösning)

den gula arean
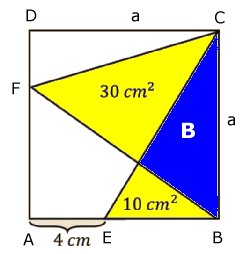
Svar:  Arean av det gula området är 28 cm2
Lösning:
Alt. 1:
 EH = DG = 5 cm.
Då är BH = 2 cm.
Arean av parallellogrammen
DEHG är 5 . 6 cm2 = 30 cm2
 Arean av triangeln BFH är
2 . 2/2 cm2 = 2 cm2
 Arean av det gula området är (30 - 2) cm2 = 28 cm2
 Alt. 2:
Arean av parallellogrammen
DIFG = 5 . 4 cm2 = 20 cm2                        
Arean av parallelltrapetset
BFIE är 2 . (5 + 3)/2 cm2 =
= 8 cm2
 Arean av det gula området är
(20 + 8) cm2 = 28 cm2
Extrauppgift:
Triangeln BFH är en likbent, rätvinklig triangeln, som är likformig med triangeln CFG. CF = 6 cm - 2 cm = 4 cm.
GC = 4 cm, eftersom triangeln CFG är en likbent, rätvinklig triangel.
Då är DC = 5 cm + 4 cm = 9 cm.
Arean av rektangeln ABCD är  9 . 6 cm2 = 54 cm2
 

 kvadratens area
Svar: Kvadratens area är 100 cm2
Lösning:
Antag att kvadratens sida är a cm samt att arean av det blå området är B cm2
Arean av triangeln BCE är
a(a - 4)/2  B + 10               (1)
Arean av triangeln BCF är
a2/2 = B + 30                     (2)
a(a - 4)/2 cm2 = B + 10
a2/2 = B + 30
Efter förenkling får man
2a = 20
  a = 10
Kvadratens area är 10 . 10 cm2 = 100 cm2

talföljder

Svar:
a) 19
b) 50, 170

Lösning:
a)
Tregrupper 1, 2, 3   4, 5, 6   8, 9, 10   13,14, 15   ?=19
Fattas   inget tal   7   11, 12   16, 17, 18  

b) 5 = 22 + 1  10 = 32 + 1   26 = 52 + 1
    Talen 2, 3 och 5 är primtal.
    Närmast följande primtal är 7, 11 och 13.
    72 + 1 = 50   112 + 1 = 122    132 + 1 = 170
 

kvadraten

Svar:
a) Den fjärde linjen har ekvationen y= 3 - x eller y = 9 - x
b) Kvadratens area är 4,5 a.e
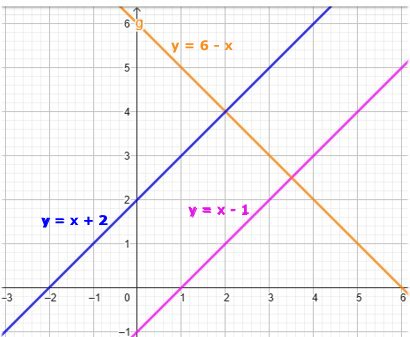
Lösning:
Den blå och den violetta linjen har k-värdet 1.
Den orangea linjen har k-värdet -1.
Då ska den fjärde linjen ha k-värde -1.

a)
Avståndet mellan skär-ningspunkterna med y-axeln för den blå och violetta linjen är 3 l.e.
Då ska avståndet från den orangea linjens skärningspunkt med y-axeln till den den fjärde linjens skärningspunkt med y-axeln vara 3 l.e.
Se nästa figur

Det finns två alternativ för den fjärde (gröna) linjen:
y = 3 - x eller y = 9 - x
(se figur).

b)
Kvadratens diagonaler är 3 l.e.
Arean är då
3.3/2 a.e. = 4,5 a.e.

 

guldmynten
Svar:  6 söner.
Var son fick 60 guldmynt.
Lösning:
Antag att Abdullah hade N guldmynt och
att varje son fick n guldmynt.
Son nr 1: n = 10 + (N - 10)/7 guldmynt        (1)
Son nr 2: n = 20 + (N - n - 20)/7 guldmynt   (2)
Alla söner fick lika många guldmynt.
Ekv. 10 + (N - 10)/7 = 20 + (N - n - 20)/7
       70 + N - 10 = 140 + N - n - 20
                  n = 60 
 n = 60 insatt i ekv. (1) ger
 60 = 10 + (N - 10)/ 7
 50 = (N - 10)/7
 N = 360

Antal söner = 360/60 = 6
 		 Problemet konstruerades av av munken Maximus Planudes omkring 1300 e. Kr.

Han var en mångsidig vetenskapsman, både framstående matematiker och språkforskare som behärskade latin och grekiska.
Tillbaka