Månadens problem februari 2023

halvcirkeln
Svar: De är lika stora Lösning: AC (diagonalen i en kvadrat) är r enligt Pythagoras sats. Triangeln ABC: BC = r (radien i halvcirkeln) och AB= 1 (radien i kvartscirkeln). Pythagoras sats på triangeln ABC ger: (r)² + r² = 1² r = Kvartscirkelns area:	Det röda områdets area: De blå områdenas area:

är professor kalkyl sexfixerad?

Svar:

Ekvationen

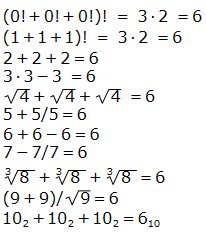Svar: t = -10
Lösning:
Staffan R. har föreslagit följande lösning:
(px + r)(x + 5) = x² + 3x + t
px² + (5p +r)x +5r = x² + 3x + t
Då är p = 1, 5p + r = 3; 5r = t; Det ger p = 1; r = -2 och t = - 10

TRIANGELN

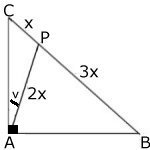
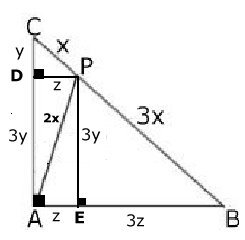
Svar: BC:AC:AB = 4:

Lösning
Alternativ 1:
Se figur.
Sinusteoremet ger:
Triangeln ACP:
x/2x = sin v/sin C
Kvadrera!
1/4 = sin²v/(1-cos²C) (1)

Triangeln ABP
3x/2x = sin (90 - v)/sin B
3x/2x = cos v/cos C
Kvadrera!
9/4 = (1-sin²v)/cos²C (2)
Bilda ett ekvationssystem av (1) och (2) och eliminera sin²v.
cos C =

AC = 4x ^.

sin C =

AB = 4x ^.= x

Lösning
Alternativ 2:
Triangeln ABC är rätvinklig.
Punkterna P, D och E delar respektive sidor i förhållandet 1:3 på grund av likformighet.
EP = AD = 3y och DP = AE = z
Pythagoras sats på trianglarna
CDP och ADP ger

y² + z² = x² (1)
9y² + z² = 4x² (2)

Efter förenkling
8y² = 3x²
y =

y-värdet insatt i ekv. (1) ger z =

BC:AC:AB = 4x: 4^.

: 4^.
Stryk x på alla tre ställena. Det ändrar inte förhålandet BC:AC:AB. Förenkla sedan.
BC:AC:AB = 4:

mynten

a)
Svar: Låda L₁ är tömd efter 4 omgångar.
Lösning: Låt 1 motsvara flytt av ett mynt från låda L₁ till låda L₂ och 2 motsvara borttagning av mynt från låda L₁.
Alice klarar uppgiften på fyra omgångar enligt följande sekvens: 1112 eller 1122
b)
Svar: Låda L₁ kan inte vara tömd efter 10 omgångar.
Lösning:
Det ligger nära till hands att anta att låda L₁ töms på minst antal omgångar, om man startar med operation 1 ett antal gånger och avslutar med operation 2 tills låda L₁ är tom (Genom att först flytta över mynt till låda L₂, kan man sedan snabbare ta bort mynt från låda L₁).
Fall 1 Antal mynt (= a) är inte ett primtal.
Man startar med att n gånger utföra operation 1.
Då finns det (a - n) mynt i låda L₁ och n mynt i låda L₂.
Antal gånger med operation 2 blir då (a - n)/n
Sammanlagda antalet omgångar: n + (a - n)/n
Ex.: a = 15 (mynt)
n + (15 - n)/n = n - 1 + 15/n = (n - 1) +15/n
n = 3 och n = 5 ger totalt 7 omgångar
Fall 2: Antal mynt (= a) är ett primtal.
n + (a - n)/n är inte ett heltal, när a är ett primtal. Formeln går därför inte att använda i det här fallet.
Använd istället den här metoden: Beräkna antalet omgångar för
(a - 1) mynt och öka sedan svaret med 1.
Sammanlagda antalet omgångar blir då n + (a - 1 - n)/n + 1

I b-uppgiften fanns det 31 mynt.
n + (a - 1 - n)/n + 1 = n + (a - 1)/n
a = 31 ger n + 30/n
n = 5 ger 5 + 30/5 = totalt 11 omgångar
n = 6 ger 6 + 30/6 = totalt 11 omgångar

Extrauppgift:
a) Svar: Låda L₁ är tömd efter 89 omgångar.
För att få så få omgångar som möjligt krävs det en lösning i fyra steg:

43 + 1 + 1 + 44 = 89 omgångar
43 + 43 + 1 + 44 ^. 44 = 2023 mynt

Lösning:
Eftersom 45 ^. 45 = 2025 inser man att det förmodligen behövs mindre än 90 (= 45 + 45) omgångar för att tömma L₁.

Det finns fyra olika alternativ, som visar att L₁ töms efter 89 omgångar.
Se figur till höger.

b) Efter att ha testat olika värden på n, kom jag fram till följande formler:
Om n = antalet mynt, och n är en jämn kvadrat (1, 4, 9, 16...) blir
antalet omgångar = (heltalsdelen av

) - 1
För övriga värden på n är antalet omgångar = heltalsdelen av

Ex.:

n = 2023
Heltalsdelen av = 89

Excelprogram som beräknar antalet omgångar

Tillbaka