Månadens problem februari 2019

nya registreringsskyltar

Svar: 38 934 400
(med det gamla systemet blev det ca 12 000 000 kombinationer)

Lösning:
Bokstäverna I, Q, V, Å, Ä och Ö får inte användas, eftersom risken för sammanblandning med andra bokstäver är stor. Då återstår det 23 bokstäver.
97 bokstavkombinationer, t.ex. FUL, är inte tillåtna.
De tre första bokstäverna kan då kombineras på 23 ^. 23 ^. 23 - 97 sätt = 12 167 sätt
Fjärde och femte tecknet kan vardera väljas på 10 sätt.
Bokstaven O kommer inte att användas som sjätte tecken, eftersom O är för likt 0 (noll)
Det sjätte tecknet kan därför väljas på 22 (bokstäver) + 10 (siffror) = 32 sätt
De tre sista tecknen kan därför kombineras på 10 ^. 10 ^. 32 sätt =
3 200 sätt.
Totala antalet kombinationer:
12 167 ^. 3 200 = 38 934 400

De mystiska gatunumren

Svar: Det lägsta gatunumret är 506
Lösning:
Eftersom vartannat nummer är udda och vartannat jämnt, måste skillnaden mellan två på varandra följande nummer vara ett udda tal.
Inget nummer förutom 555 får innehålla två lika stora siffror. Därför kan skillnaden mellan två på varandra följande nummer inte vara 1, 3 eller 5 (Vi skulle få gatunumren 554, 552 resp. 550)
Vi testar därför om skillnaden är 7:
597 590 583 576 569 562 555 548 541 534 527 520 513 506
Anm.: Skillnaden 9 mellan gatunumren fungerar inte
618 609 600 591 582 573 564 555 546 537 528 519 510 501
Gatunumren ska ju ligga intervallet 500 - 599.

Cirklarna

Svar: 120 gånger
Lösning:

Tid	A	B
1/4 min	1/2 varv	3/2 varv
3/4 min	3/2 varv	9/2 varv
5/4 min	5/2 varv	15/2 varv
7/4 min	7/2 varv	21/2 varv
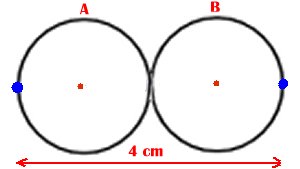
osv. Av tabellen framgår att avstån-det är exakt 4 cm två gånger per minut. 60 ^. 2 = 120

Priset för en kyckling

Svar: En kyckling kostade 4 kr
Lösning:
Ett problem från Skolornas matematiktävling.

Antag att de köpte n hönor och att priset för en kyckling var y kr.

Fakta i uppgiftstexten:
x får kostar x kr/st

försäljningssumman är x² kr
en höna kostar 12 kr

n hönor kostar 12n kr
"lika många djur"

antalet hönor är udda
"de pengar som återstod"

1 ≤ y ≤ 11

Ekv.: x²= 12n + y

Det räcker att undersöka x = 1, ... 12 enligt lösningarna i "Skolornas matematiktävling":
"Eftersom ( x+12)² = x² + 12(2x+12) är det klart att två x-värden som har skillnaden 12 ger samma y-värde och samma paritet på n. Vi behöver därför bara undersöka x = 1, ... 12"