Månadens problem februari 2018

Xi Enting

Svar: Två sorters grönt te
Lösning:
För två av kopparna kan Xi Enting välja mellan sju olika sorters te. Därför finns det enligt multiplikationsprincipen 2 · 7 = 14 olika sätt att kombinera tesort och tekopp. Då finns det 16 − 14 = 2 sätt för koppen som bara ska användas till grönt te. Alltså har Xi Enting två sorters grönt te.

professor kalkyls 30-årsdag

Svar: 270
Lösning:

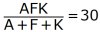
Eftersom 30 är delbart med 10, måste det tresiffriga talet AFK vara delbart med 10. Det betyder att K = 0.
Värdet av det tresiffriga talet AFK är 100A + 10F + K (men K= 0)
Villkoret kan därför skrivas

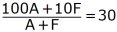eller enklare

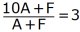
Vi löser denna ekvation:
10A + F = 3A + 3F
7A = 2F Den enda heltalslösningen är A = 2 och F = 7

ett årsaktuellt problem

Det gäller att dela upp årtalet (a) i faktorer (Även a = 1 ^. a måste undersökas)

Svar: Det finns inte någon positiv heltalslösning till p² - q² = 2018

Lösning:
p och q är positiva heltal.
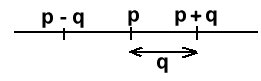
p² - q² kan skrivas ( p + q)(p - q)
Av figuren till höger framgår att antingen är
p -q och p + q båda udda tal, eller är båda jämna tal.
Fall 1:
p + q och p - q är båda udda tal.
Då är produkten ( p + q)(p - q) ett udda tal och alltså ingen lösning till
p² - q²= 2018
Fall 2:
p + q och p - q är båda jämna tal.
I så fall är produkten ( p + q)(p - q)
delbar med 4.
Men talet 2018 är inte delbart med 4.
Fall 2 är inte en lösning till p² - q²= 2018

Extrauppgift:
a)
Svar: p = 1009 och q = 1008
Lösning: p² - q²= 2017      2017 är ett primtal.
Enda möjligheten är
p + q =2017
p - q = 1
p = 1009 och q = 1008

b)
Svar: p² - q²= 2019 har två lösningar p = 338 och q = 335
                                                    p = 1010 och q = 1009
Lösning:
2019 = 3 ^. 673
p + q = 673
p - q = 3
p = 338 och q = 335

2019 = 1 ^. 2019
p + q = 2019
p - q = 1
p = 1010 och q = 1009

c)
Svar: p² - q²= 2020 har två lösningar p = 506 och q = 504
                                                    p = 106 och q = 96
Lösning:
2020 = 2 ^. 1010
p + q = 1010
p - q = 2
p = 506 och q = 504

p + q = 202
p - q = 10
p = 106 och q = 96

Slutsats:
För primtal >2 finns det en lösning
För övriga udda tal finns minst två lösningar
För årtal med sommar-OS finns det minst en lösning (t.ex. 2012) men ibland betydligt flera (2016 har 12 lösningar)
Övriga jämna årtal saknar lösning

liksidiga trianglar

Svar: 5/24Lösning:
Triangeln ABC är enligt uppgiften uppdelad tre likbenta trianglar (ABP, ACP och BCP).
Eftersom D, E och F är mittpunkter på sidorna, är triangeln ABC uppdelad i fyra kongruenta trianglar (ADE, BDF, CEF och DEF).
Triangeln ACP är därför 1/3 av triangeln ABC:s area.
Triangeln CEF är 1/4 av triangeln ABC:s area. Då är den gula triangeln 1/8 av triangeln ABC:s area.

Det röda områdets area är

av triangeln
ABC:s area.