|
problem från holland |
|
rembrandt |
Svar:
Robert har ingen tavla, som är
målad av Rembrandt
Lösning:
Vi vet att endast en av de tre vännerna hade rätt.
Om Adam hade rätt ("åtminstone fyra"), skulle också David ha
rätt ("åtminstone en").
Om David hade rätt ("åtminstone en"), skulle också Adams
("åtminstone fyra") eller Bertils påståenden ("färre än fyra")
vara rätt.
Om endast Bertil har rätt ("färre än fyra"), måste det innebära,
att David ("åtminstone en") har fel. David har fel, om Robert
inte har någon Rembrandt-
tavla! |
|
holländsk MA-tävling |
Svar:
Förhållandet är 1:3 (1/3)
Lösning:
F är medelpunkt för halvcirkeln.
Triangeln ABC skär halvcirkeln i punkterna D och E |
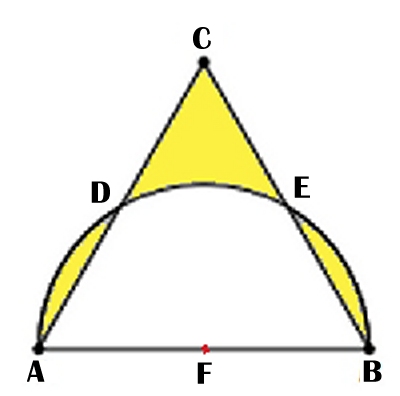 |
Man inser att trianglarna BEF, ADF,
DEF och CDE är likformiga och kongruenta med sidan 6 cm.
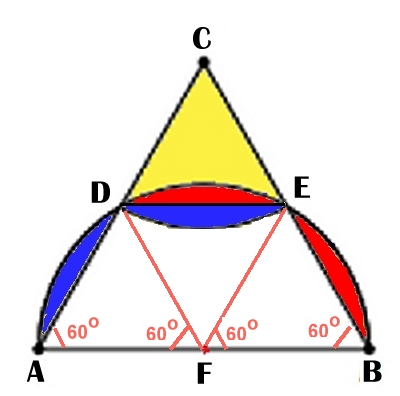
Man inser också att det blå segmentet till vänster om AD är lika
stort som det blå segmentet under DE. Det röda segmentet till
höger om BE är lika stort som det röda segmentet ovanför DE.
De gula områdena i den översta figuren kan alltså ersättas av
cirkelsektorn CDE med C som medelpunkt.
Men cirkelsektorn CDE är lika stor som cirkelsektorn FDE med F
som medelpunkt.
Cirkelsektorn FDE är 1/3 av halvcirkeln! |
 |
|