|
Räkna med Ryssland del
1 |
|
Några
problem från den ryska matematikundervisningen |
Uppg. 1:
Svar:
Kl. 06.00
Lösning:
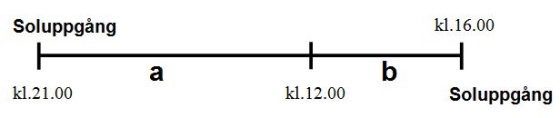
Den första kvinnan går sträckan b (km) på fyra timmar
(kl. 12 till kl. 16).
Hennes hastighet är därför b/4 km/h (kl. 12 till kl. 21).
Den andra kvinnan går a (km) på nio timmar
Hennes hastighet är därför a/9 km/h.
Tiden för den första kvinnan att gå från soluppgången till kl.
12.00 är
a/(b/4) timmar = 4a/b timmar
Tiden för den andra kvinnan att gå från soluppgången till kl.
12.00 är
b/(a/9) timmar = 9b/a timmar.
Dessa båda tider (från soluppgång till kl. 12.00), som är lika
stora, ger ekvationen
4a/b = 9b/a
4a2 = 9b2 Lösning av den här
andragradsekvationen ger
2a = 3 b
a = 1,5b
Den andra kvinnans hastighet kan då skrivas
a/9 = 1,5b/9 = b/6
(km/h)
Tiden för henne att gå sträckan b blir då b/(b/6) = 6 (timmar).
Det betyder att soluppgången inträffade kl. 12.00 - 6 timmar =
kl. 06.00 |
Uppg. 2:
Svar:
Strömhastigheten är 3 km/h.
Lösning:
Den enklaste lösningen får vi, om vi väljer det system som
följer floden.
I detta system är flaskan i vila så fort den är tappad. Simmaren
simmar först iväg ifrån den, för att senare simma
tillbaka. Simmarens simhastighet antas konstant, så det tar lika
lång tid för honom att simma i bägge riktningarna i det medflytande systemet. Ena vägen tog 20 minuter, så den andra
vägen måste också ha tagit 20 minuter, vilket innebär att
flaskan var borttappad under 40 minuter. Om vi istället ser vad
som händer med flaskan med avseende på stranden, finner vi att
det tog 40 minuter för flaskan att flyta fram från den ena bron
till den andra, dvs. 2 km. 2 km på 40 min motsvarar 3 km på en
timma. Strömhastigheten är 3 km/h. |
|