Lätt:
Svar:
12
Lösning:
Differensen av medelvärdena är 12 - 9 = 3
Eftersom man beräknar medeltalet av fyra tal, kommer det största
resp. det minsta talet att divideras med 4. Differensen mellan
det största och minsta talet är därför 4 gånger så
stort som differensen av medelvärdena, dvs. 12. |
Medel:
Svar:
60 %
Lösning:
Antag att gruppen består av a personer, varav x män.
Då finns det (a - x) kvinnor i gruppen.
Ekv.:
35x + 25(a - x) = 31a
10x = 6a
x/a = 0,6 dvs. 60 % |
Svår:
Svar:
a) 55
b) 1
Lösning:
a) Summan av talen på lapparna är 1 + 2 + ... 10 = 55.
Antag att personerna valt talen a, b, c, d, e, f, g, h, i och j.
Summan av talen på lapparna blir då (a + c)/2 + (c + e)/2 + (e +
g)/2 +
(g + i)/2 + (i + a)/2 + (b + d)/2 + (d + f)/2 + (f + h)/2 + (h +
j)/2 +
(j + b)/2 = 2(a + b + c + d + e + f + g + h + i + j)/2 =
= a + b + c + d + e + f + g + h + i + j dvs. summan av talen på
lapparna är densamma som summan av de tal som de tio personerna
valde.
I ord blir resonemanget så här: Det tal som en person har valt
ingår i medelvärdet på de två grannarnas lappar. Eftersom man
vid medelvärdet delar med 2, blir resultatet att de tio
personernas tal räknas med en gång. Summan av de tio personernas
tal är därför lika med summan av talen på lapparna, dvs. 55.
b) Eftersom
vi har tio variabler kan vi bilda ett
ekvationssystem med tio ekvationer.
För att ta reda på värdet av a räcker det dock med fem
ekvationer:
a + c = 14
c + e = 18
e + g = 2
g + i = 6
i + a = 10
Genom att lösa ekvationssystemet får vi
a = 1 |
 |
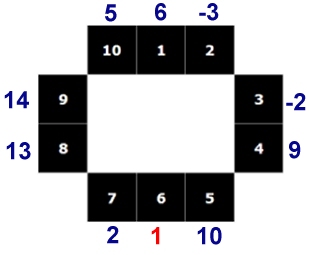
Av figuren till höger framgår vilka tal de tio personerna
tänkte på. |
 |
|
|