Påskgodis

Svar: 8 kycklingar

Lösning:
Antag att det från början fanns x kycklingar och 2x hönor.
När ytterligare två kycklingar tillkommit var det sammanlagda antalet djur i hönsgården
2x + x + 1 + 2. Efter förenkling får man 3x + 3, vilket kan skrivas 3(x + 1)
Två villkor ska uppfyllas:
1) Summan skall vara jämnt delbar med 7. Det betyder alltså att (x + 1) måste vara delbart med 7.
Två värden som uppfyller villkoret är x= 6 och x = 13. Vi undersöker om dessa värden också uppfyller villkor nr 2.
2) Summan skall vara mindre än 40.
x = 6 3(x + 1) = 3 ^. 7 = 21
x = 13 3(x + 1) = 3 ^. 14 = 42 Duger inte!

Antalet kycklingar är alltså 6 + 2 = 8

Tillbaka

Svar: Ja (100 000 s istället för 86400 s)
Tillbaka

Påskliljor och tulpaner

Svar: 10 tulpaner
Lösning:

Fall 1:

Fall 2: Av figurerna framgår att de 30 tulpaner som rådjuren åt upp, motsvarar 3/4 av tulpanerna.
1/4 av tulpanerna återstår, dvs. 10 tulpaner.
Anm.: Naturligtvis kan man också lösa problemet med ekvation.

Tillbaka

Påskäggen I

Svar: Ja, Fredrik och hans mamma, som är datafreak, räknade i det hexadecimala systemet.
12₁₆ = (16+2)₁₀ = 18₁₀Tillbaka

Påskäggen II

Erik har fått i uppgift att koka påskäggen i 7 minuter. Han har två timglas, som visar tiden 5 resp. 3 minuter. Hur skall han göra?
Lösning:
1) Vänd båda timglasen samtidigt.
2) När 3 min-timglaset runnit ut, vänds detta på nytt.
3) När 5 min-timglaset runnit ut, har 3 min-timglaset runnit i 2 min.
4) Vänd 3 min-timglaset på nytt, så tar det 2 min för det att rinna ut.
5 min + 2 min = 7 min
Tillbaka

Kryptot

Svar: MED ELD I BAKEN

Anm. 1: Bokstäverna har förskjutits 20 steg.
Anm. 2: Caesarkryptot är lätt att knäcka, eftersom det endast finns 27 olika varianter (p.g.a. att det är 28 bokstäver i alfabetet) att undersöka.
Med ett kalkylprogram kan man snabbt ta fram alla dessa varianter.

Tillbaka

Påskdekorationen

Svar: 64

cm » 201cm

Lösning:
Vi kallar cirklarnas diametrar d₁, d₂, d₃.....d₇Den totala omkretsen blir då (

^.d₁+

^.d₂+

^.d₃+

^.d₄+

^.d₅+

^.d₆+

^.d₇) cm =

(d₁+d₂+d₃+d₄+d₅+d₆+d₇) cm
Men d₁+d₂+d₃+d₄+d₅+d₆+d₇ är enligt uppgiften 64 cm.
Omkretsen är därför 64

201cm

Tillbaka

Påskkycklingarna

Svar: En tupp, sex hönor och 13 kycklingar
Lösning:
Antag, att man köpte x tuppar och y hönor.
Ekv.:
12x + 8y + 5(20-x-y) = 125 Efter förenkling får man x = (25-3y)/7
Eftersom endast heltalslösningar duger, är y=6 den enda lösningen.
Då blir x=1 och antalet kycklingar, dvs. (20-x-y)=13
Tillbaka

Påskdagen

Svar: Påskdagen kan tidigast infalla den 22/3
(senast 1818 och nästa gång 2285)
Påskdagen kan infalla senast 25/4 (senast 1943 och nästa gång 2038)
Tillbaka

Farmors karamellskål

a) Svar: Sju barnbarn var på besök.
Antag att antalet barnbarn är n st.
Varje barnbarn får då 1/n av totala antalet kolor. Eftersom minsta barnbarnet fick 1/6 resp. 1/8 av av de olika sorterna, så gäller att 6<n<8, dvs. n=7.

b) Svar: En lösning är sex Dumlekolor och åtta Dajmkolor. En annan lösning är 12 Dumlekolor och 16 Dajmkolor.
Allmänt:
Antag att det fanns a st Dumlekolor och b st Dajmkolor.
Ekv.:

Efter förenkling får man att

Minsta antalet kolor som uppfyller detta villkor och samtidigt ger det minsta barnbarnet hela kolor är sex Dumlekolor och åtta Dajmkolor.
Rent allmänt skulle man kunna skriva lösningen så här:
Det fanns sammanlagt 6^.k st Dumlekolor och 8^.k st Dajmkolor. k= 1,2,3...
Tillbaka

Påskelden

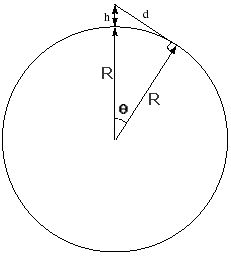
Svar: Ca 25 km
Lösning:
Man kan använda Pytagoras sats, eftersom differensen mellan avståndet d (se fig.) och avståndet längs jordytan är försumbart.
R = jordens radie h = påskeldens höjd
Enl. Pytagoras sats är

R ≈ 6370 km och h = 50 m ger d ≈ 25,23891 km
längden (l) längs jordytan är R^.Ө ≈ 25,23878 km
dvs. d - l ≈ 13 cm (!).
Ө = arccos(R/(R+h)

Tillbaka

Resan till Blåkulla

En lösning kan se ut så här:
Årets hastighet är 5/6 av fjolårets hastighet Û fjolårets hastighet är 6/5 av årets hastighet.
Antag, att hastigheten det här året var x km/h.
Sträckan betecknas med a km
Förra året kom häxan till Blåkulla kl. 22.22. I år anlände hon kl. 23.32.
Förra året gick alltså resan 70 min (7/6 h) snabbare.
Ekv.:

x = a/7
Eftersom bränslet räckte för ca 640 km och marginalerna var små, bör avståndet till Blåkulla ha varit obetydligt kortare, kanske 630 km. I så fall blir hastigheten 630/7 km/h = 90 km/h
Tillbaka

Landningen

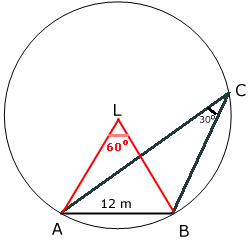
Svar: 12 m
Lösning:
Eftersom reservlandningsplatserna ligger lika långt från den bästa landningsplatsen (L), ligger A, B och C på periferin till den cirkel, som ritas med L som medelpunkt och LA som radie. (se fig.)
Periferivinkeln BCA är 30^o. Då är medelpunktsvinkeln ALB 60^o. Det medför att triangeln ABL är liksidig, dvs. LA och LB (liksom LC) är 12 m.

Tillbaka

Parkeringsplatsen

Svar: Kvastarna kunde byta plats på 44 sätt.

Generell lösning:
Uppgift: n st kvastar placerade på n st parkeringsplaser skall placeras om så att ingen kvast finns kvar på sin ursprungliga plats. På hur många olika sätt kan detta göras?
Svar: En formel för att beräkna antalet sätt kan skrivas så här:
n! (1/2! - 1/3! + 1/4!... + (-1)^{n .}1/n!)

Specialfallet n = 5
n=5 ger 5!(1/2! - 1/3! + 1/4! -1/5!) = 120(1/2 - 1/6 + 1/24 -1/120)=60 - 20 +5 -1 = 44