Månadens problem
december 2024 (lösning)

 additionen
Svar: 272 + 272  +  272 = 37 eller (-27)2 + (-27)2  + (-27)2 = 37
Lösning:
Antag att varje term är x2
Då får vi x2 + x2 + x2 = 37
            3x2 = 37
                 x2 = 36
                  x = ±33 = ±27
Två lösningar: 272 + 272  +  272 = 37 eller (-27)2 + (-27)2  + (-27)2 = 37
 

 beviset
 
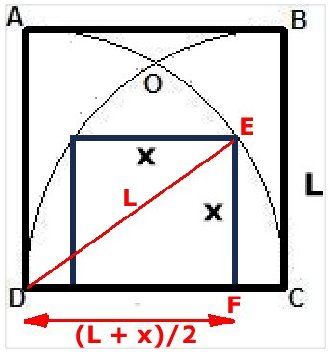
Bevis:
Sträckan DE = DC = L
(radie i en av kvartscirklarna)
Sträckan FC = (L - x)/2
Då är sträckan DF = L - (L - x)/2 =
= (2L - L + x)/2 = (L + x)/2

Pythagoras sats på triangeln DEF ger:
x2 + ((L + x)/2)2 = L2

4x2 + L2 + 2Lx + x2 = 4L2
5x2 + 2Lx - 3L2 = 0
x2 + 2Lx/5 - 3L2/5 = 0

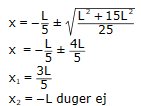
V.S.B.

 den vita halvcirkeln
Svar: Halvcirkeln täcker 8/25 =
32 % av den blå cirkeln
Lösning:
Antag att radien i halvcirkeln är r.
Enligt kordasatsen får vi då
r . r = 2(r + 4)
r2 = 2r + 8
Andragradsekvationen ger lösningen
r = 1 ± 3
Eftersom radien > 0 duger endast
lösningen r = 4 cm

Radien R i cirkeln blir då
(2 + 4 + 4)/2 cm = 5 cm

Halvcirkelns area = . r2/2 =
. 42/2 cm2 = 8 cm2
Cirkelns area = . r2 =
. 52/2 cm2 = 25 cm2
Halvcirkeln täcker 8/25 = 8/25 =
32 % av den blå cirkeln.
 

julfesten 
a) Svar: Julfesten ska anordnas i by C.
Då blir den totala resvägen i ena riktningen 800 km.
Lösning:


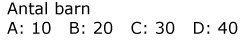
Totala resvägen (enkel resa) om julfesten äger rum i
A: (0 + 200 + 600 + 1200) km = 2000 km
B: (100 + 0 + 300 + 800 km = 1200 km
C: (200 + 200 + 0 + 400) km = 800 km
D: (300 + 400 + 300 + 0) km = 1000 km

b) Svar: Den totala resvägen är kortast om festen anordnas i by C.
Lösning:
Det ligger nära till hands att anta att den kortaste totala resvägen antingen inträffar om festen äger rum i by C, eller i närheten av by C, eftersom de flesta barn bor i by D och by C.
Vi undersöker de två alternativ, som är tänkbara, om inte by C ger den kortaste totala resvägen:
Alt. 1:
Antag att festen äger rum mellan by B och by C, x km från by C

Sammanlagt antal km för barnen i
A: 10(20 - x)
B: 20(10 - x)
C: 30x
D: 40(10 + x)
Sammanlagt för alla barnen: 800 + 40x
Slutsats: Kortaste totala resvägen får man, om x = 0, dvs. att festen äger rum i by C.

Alt. 2:
Antag att festen äger rum mellan by C och by D, y km från by C

Sammanlagt antal km för barnen i
A: 10(20 + y)
B: 20(10 + y)
C: 30y
D: 40(10 - y)
Sammanlagt för alla barnen: 800 + 20y
Slutsats: Kortaste totala resvägen får man, om y = 0, dvs. att festen äger rum i by C.
 		  

  vikningen
a) Svar: Punkten F ligger 9 cm från B.
b) Svar: Sträckan FG är ungefär 15,6 cm

Man inser att om hörnet B vid vikningen ska hamna på sidan AD, så ligger BF i intervallet 6 cm < sträckan BF ≤ 12 cm.
Se figur nedan till vänster:
FB = x = FE
Då är AF = 12 - x
Pythagoras sats på triangeln AEF ger efter förenkling att AE =
Eftersom vinkeln FEG är rät, är trianglarna AEF och HGE likformiga enligt vinkelbeteckningarna i figuren.
(Motivering: Trianglarna AEF och HGE rätvinkliga. Vinkelsumman i en triangel är 180o, och de tre vinklarna vid E bildar ett halvt varv = 180o.)

Likformighet ger:
       

Pythagoras sats på BFG ger: z2 = x2 + y2
  Eftersom    får man efter förenkling 
Alt. 1: Derivera z för att få fram minimivärdet för sträckan FG.
          När derivatan sätts lika med noll, blir x = 9.
Eftersom deriveringen ger rätt jobbiga uträkningar, är det enklare att använda alt. 2.
Alt. 2: Ta fram grafen till z (se figur nedan till höger)
Gör så här:
Skriv funktionen z = (x^3/(x - 6))^0.5 i adressfältet i webbläsaren, så visas grafen.
Om man ställer muspekaren på grafens minimipunkt visas koordinaterna (9, 15.588)
Kontroll: x = 9 =>

extrauppgift: offerfesten
Lösning:
11. Dxh6!, Txh6
12. gxh6, Sf8
13. Sf6†, Ke7
14. d5, Da5
15. d6 Kd8
16. h7, Dxa2
17. h8D, Sb-d7
18. Dxf8†!, Sxf8
19. Th8
Svart gav upp (SM-parti i Bollnäs 1973)
 		 Analys: https://www.365chess.com/board_editor.php

Vits båda damer försvann.
Ändå var det vit som vann!
 

Tillbaka