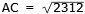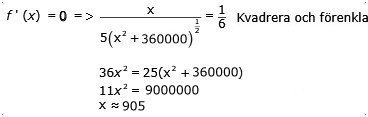Månadens problem
december 2023 (lösning)

russinen
Svar: Han hade 54 russin
Lösning:
Alt. 1
Antag att Alfred hade x russin.
a)
• • •
Han gav bort 1/3 av russinen till Alice. Då återstår 2x/3 russin.
Han åt 4 russin. Då återstår (2x/3 - 4) russin.
Han gav bort hälften av återstående russin till Maja. Då återstår (2x/3 - 4)/2, vilket är 16 russin enligt uppgiften.

Ekv.: (2x/3 - 4)/2  
             2x/3 - 4
              2x - 12 
                     2x
                       x 

=
=
=
=
=		 16
32
96
108
54
b) Alfred fick (4 + 16) = 20 russin, Alice fick 54/3 russin = 18 russin och Maja fick 16 russin
Alt. 2
 Birger J har föreslagit en lösning utan ekvation:
 Innan Maja fick hälften (dvs. 16 st) hade Alfred 32 russin.
 Han hade 36 (32+4) russin efter att han givit Alice 1/3
 36 russin var 2/3 av totala antalet vilket var 54 russin.
 Maja fick 16 russin Alice 18 (36/2)russin och Alfred 20 (16+4) russin
 

tre okända tal

Svar: x = 674, y = 2 och z = 675

Lösning:  
xy + z = 2023 (1)
x + yz = 2024 (2)
 		 x, y och z är naturliga tal.
Bestäm värdet av x, y och z.
Subtrahera ledvis ekv. (2) och (1)
x + yz - (xy + z) = 2024 - 2023
x + yz - xy - z    = 1
y(z - x) -1(z - x) = 1
(z - x)(y - 1) = 1       (3)
Produkten 1 får man av 1 . 1 eller (- 1) . (- 1). Men y > 0, så y - 1 = 0 - 1 = - 1 duger inte.
y - 1 = 1 => y = 2    Då måste z = x + 1 enligt ekv. (3)
Ekvation (1) kan skrivas 2x + x + 1 = 2023 när vi ersätter y med 2 och z  med x +1.
3x = 2022
  x = 674
  z = x + 1 = 675
 

renen rudolf
a)
Svar: Kvadratens area är 1156 m2.
 Lösning:
 Fig. 1:
Sträckan 28 m från hörnet A förlängs till punkten E.
EF är parallell med CG = 18 m.
Då är AE = 28 m + 18 m = 46 m.
CE är parallell med GF = 14 m

Fig. 2:
Diagonalen AC beräknas med Pythagoras sats.
(AC)2 = 462 + 142
(AC)2 = 2312




 

 
   

flugan
a)
Svar: Om flugan befinner sig i diagonalernas skärningspunkt på golvet bör hon på grund av symmetrin befinna sig där summan av kvadraterna på dess avstånd från takets fyra hörn är så liten som möjligt.
Kontroll:
Flugan är i punkten J
Avståndet (JE)2 = (JF)2 = 6 (Pythagoras sats AEJ resp. BJF)
Avståndet (JG)2 = (JH)2 = 6 (Pythagoras sats CGJ resp. DHF)
Summan blir 4 . 6 = 24
b)
Svar: Om flugan befinner sig i ett av hörnen på golvet bör hon på grund av asymmetrin befinna sig där summan av kvadraterna på dess avstånd från takets fyra hörn är så stor som möjligt.

 
Kontroll:
Flugan är i ett av golvets hörn, t.ex. A
Avståndet (AE)2 = 22 = 4  
Avståndet (AF)2 = (AH)2 = 8
Avståndet (AG)2 = 12
Summan blir 4 + 8 + 8 + 12 = 32
Ytterligare kontroll: Flugan befinner sig mitt på en kant (punkten K) i basytan.
Avståndet (KE)2 = (KF)2 = 5  avståndet (KG)2 = (KH)2 = 9
Summan blir 5 + 5 + 9 + 9 = 28
 

 slädfärden
Svar: Punkten B ligger ungefär 495 m från punkten A.
Genom att efter punkten B ta genvägen till D, blir tiden 300 s.
Tiden för att åka den plogade vägen AC-CD är 2000/6 s ≈ 333 s
Tidsvinsten blir 33 s. Det är frågan om den lilla tidsvinsten motiverar att ta den besvärligare genvägen över sjön.
Lösning:
 Antag att sträckan BC är x m.
Då är sträckan AB = (1400 - x) m och sträckan BD = (x2 + 6002)1/2
Tiden för sträckan AB-BD blir 
f(x) = (1400  - x)/6 + (x2 + 6002)1/2/5
Vi kan behandla det här uttrycket som ett max- och minproblem, dvs. derivera uttrycket och sedan sätta derivatan lika med noll.
Sträckan AB 1400 m - 905 m = 495 m
 Sträckan BD beräknar vi med Pytagoras sats till ungefär 1086 m
 Tiden blir 495/6 s + 1086/5 s ≈ 300 s

Tillbaka