Månadens problem december 2022

marknaden i bagdad

Svar:
a) Ali hade vikterna 1, 2, 4 , 8, 16 hg
(1, 2, 4 , 8, 16 är positionernas värde från höger till vänster i det binära talsystemet).
Han kan då väga alla heltal (enhet hg) från
1 till 31 (1 + 2 + 4 + 8 + 16 = 31)
b) Mustafa hade vikterna 1, 3, 9, 27 hg
(1, 3, 9, 27 är positionernas värde från höger till vänster i det trinära talsystemet, dvs. talsystemet med 3 som bas).
Han kan då väga alla heltal (enhet hg) från
1 till 40 (1 + 3 + 9 + 27 = 40) , under
förutsättning att han för en del vägningar får sätta vikter på båda vågskålarna.
Ex.: För att väga 15 hg, sätter han 27 hg på den ena vågskålen och 9 hg och 3 hg på den andra vågskålen.
Anm.: I det trinära talsystemet skrivs 15_{bas 10} så här: 120_{bas 3}

intelligenstestet

Svar: 581
Lösning:

Svar:
9   (45)    81
8   (36)    64
10   (55) 100
Lösning:
Talet till höger om parentesen är kvadraten av talet till vänster.
Talet i parentesen är hälften av summan av talen utanför parentesen.

skidspåret
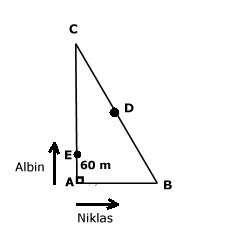
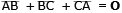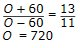
a) Svar: Skidspåret är 720 mLösning: Eftersom de möts i mittpunkten D på hypotenusan, måste Albin som har högst hastighet ha börjat längs den längsta kateten. Andra gången möts de i punkten E Triangelns omkrets = (m) Total sträcka vid andra mötet Albín: O + 60 (m) Niklas: O - 60 (m) Dessa sträckor förhåller sig som 13:11 Skidspåret är alltså 720 m
b) Svar: Albin har åkt 9360 m och Niklas 7920 m Lösning: När de möts i punkten E har mötespunkten jämfört med startpunkten förflyttats 60 m. De har då möts 2 gånger. Skidspåret är 720 m enligt a-uppgiften. 720/60 = 12 När de möts i startpunkten, har de möts 12 ^. 2 = 24 gånger Mellan två möten har Albin åkt 13 ^.720/24 m = 390 m och Niklas 720 m - 390 m = 330 m Albin har åkt sammanlagt 24 ^. 390 m = 9360 m och Niklas 24 ^. 330 m = 7920 m

fyrhörningen
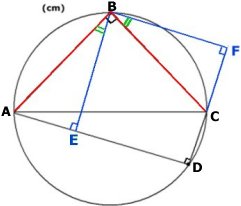
Svar: Avståndet från B till AD är 4 cm. Lösning: Vinkeln ABC och vinkeln D är räta vinklar (randvinklar på en halvcirkelbåge). DC förlänges så att vinkeln BFD är rät. Då är även vinkeln EBF rät. B är mittpunkt på cirkelbågen ABC. Då är AB = BC. Av figuren framgår att vinkeln ABE = 90^o - vinkeln EBC och vinkeln CBF = 90^o - vinkeln EBC, dvs.vinkeln ABE = vinkeln CBF Då är trianglarna ABE och CBF kongruenta. Därav följer att BE = BF och arean av kvadraten DEBF är lika stor som arean av fyrhörningen ABCD = 16 cm²och BE är 4 cm.

renarna

Svar: Tomtefar har 2025 renar
Lösning:
Antag att tomtefar har n renar och att k st av dem finns i vinterbete A.
I vinterbete B finns då (n - k) renar.
Sannolikheten att tomtefar väljer ut två renar från olika vinterbeten är då

gula arean

Svar: Arean är ca 5,0 cm² Lösning:
O är cirkelns medelpunkt.
Triangeln ABE är liksidig och triangeln ABO är en likbent rätvinklig triangel.
Därför är vinkeln OBE = 60^o-45^o=15^oSträckan BO = cm
och sträckan EO = (

- 2) cmVinkeln BOE = 180^o - 15^o - 60^o/2 = 135^o
1) Det streckade området OEF är lika med arean av sektorn BEF - triangeln BEO
2) Det gula kvadratliknande kan delas upp i 8 områden som är lika stora som det streckade området OEF.
Alltså är det ursprungliga gula området 8 gånger så stort som det streckade området OEF.
Arean av cirkelsektorn BEF =

Arean av triangeln BEO beräknas med formeln

Arean av det gula området:

Tillbaka