|
TOMTENS JULKLAPPSSÄCK |
Svar: Tomten har 74 julklappar i
sin säck.
Lösning:
1) Om tomten hade haft ytterligare en julklapp, hade
antalet varit delbart med 5.
Det innebär att antalet julklappar i säcken måste ha entalssiffran 4
eller 9.
2) Tiotalssiffran kan inte vara ett jämnt tal, för i så fall skulle man
inte få ett primtal, när man kastar om siffrorna.
3)Tiotalssiffran kan inte heller vara talet 5, för i så fall skulle man
inte få ett primtal, när man kastar om siffrorna. |
 |
Vi ska alltså undersöka talen 34, 39, 74, 79, 94 och 99.
Av dessa tal är det 34, 74 och 79 som blir
primtal, om man kastar om siffrorna.
4) Om tomten hade haft en julklapp mindre, hade antalet
varit ett primtal.
Talet 74 - 1 = 73 är ett primtal!
|
|
|
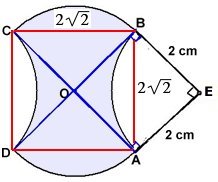
silversmycket |
a)
Villkor:
Endast om EA och EB är tangenter till den nedre resp. övre
cirkelbågen finns det en entydig lösning till de här
uppgifterna.
Lösning:
EA och EB är tangenter och bildar 90 grader med radien till
tangeringspunkten.
Då är vinkeln AOB = 360 - 3*90 = 90 grader (fyrhörningen ACBO)
Då är radierna OA och OB också 2 cm och medelpunktsvinkeln för
varje sektor är 90 grader.
Då är de fyra cirkelbågarna lika stora.
b) Arean är 8 cm2
Lösning:
AB = BC = CD = DA =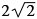 
cm (Pythagoras sats)
Genom att flytta övre och nedre cirkelsegmenten
inser man att arean =
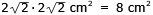
c) Omkretsen är 4 cm ≈ 12,6 cm
Lösning:
Cirkelbågarna bildar tillsammans omkretsen av en cirkel.
O =
. d
O =
.
4 cm ≈ 12,56 cm
|
 |
|
|
god jul! |
Svar: J = 4, U = 6, L
= 1, M = 5, Y = 3, S = 8
Lösning:
7(JULMYS) = 6(MYSJUL)
Ersätt det tresiffriga talet JUL med x och det tresiffriga talet MYS med y
Ekv.: 7(1000x + y) = 6(1000y + x)
6994x = 5993y Dividera båda leden med 13
538x = 461y Går ej att förenkla mer, eftersom 461 är ett
primtal.
Slutsats: Eftersom x och y är heltal, måste x = 461 och y = 538
J = 4,
U = 6, L = 1, M = 5, Y = 3, S = 8 |
|
|
|
multiplikationen |
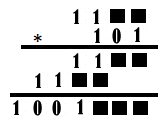
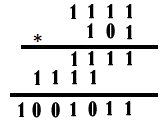
a) Svar: 1111 . 101
= 1001011
Lösning:
Talen på varje rad börjar med en etta.
Produkten på fjärde raden är
förskjuten två steg. Då är andra siffran på andra raden 0.
Produkten innehåller sju siffror.
Genom resonemang om nödvändiga minnessiffror kan man komma fram till att andra
siffran i översta raden är 1 och att andra och tredje siffran i svaret är
0 (figuren
överst till höger).
Men fjärde siffran i svaret kan bli 1, endast om de två sista siffrorna på
första raden är ettor. (Se figur till höger)
|
 |
|
b) Svar:
Talsystemet har
basen 8
(Oktala
systemet) |
Lösning:
1001011(bas 2) = 26 + 23 + 21
+ 20
= 64+8+2+1 = 75(bas 10)
Antag att det nya talsystemets bas är x
1 . x2
+ 1 . x1 + 3 . x0
= 75
x2
+ x + 3 = 75
x2
+ x - 72 = 0
 |
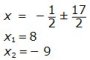c) Svar:
I datorer
Det oktala talsystemet har använts vid programmering av datorer.
Numera det hexadecimala
talsystemet
(talsystem med basen 16) vanligare vid datorprogrammering.
Folkslag som räknat med det oktala talsystemet
Man tror att de inte räknade på fingrarna utan på mellanrummet mellan
fingrarna (ursprungsfolket Yuki i Kalifornien) eller på knogarna i
stängda nävar (folk i Mexiko som talade språket Pame)
Karl XII och Swedenborg
Karl XII ville införa ett talsystem med basen 64, men Swedenborg avrådde
honom. Man skulle visserligen kunna skriva stora tal med få siffror, men
talsystemet skulle å andra sidan innehålla 64 olika tecken för siffror och det
skulle bli besvärligt för "personer med ringare fattningsförmåga än Ers
Majestät", sade Swedenborg.
Istället rekommenderade han det oktala talsystemet,
men det kom aldrig användas i Sverige.
|
|
|
mattelektionen |
|
|
|
och cos v=
