Svar:
Tomtenissen hade fel.
Lösning:
Vedklamparna har fortfarande samma längd som i standardbunten. Det som har
ändrats är buntens omkrets och därmed också arean på bunten.
Volymen på veden är proportionell med buntens area.
Omkretsen är proportionell mot radien, men arean är proportionell mot radien i
kvadrat.
När omkretsen är 1,5 gånger större, är arean (1,5)2 =
2,25 gånger större.
I själva verket var det alltså mer än dubbelt så mycket ved i den nya bunten. |
 |
|
Svar:
Alt. 1:
Lådan har avrundat måtten 5,6 x 5,6 x 3,2 (dm) Den totala yttre arean av lådan ≈ 102,82 dm2
Alt. 2:
Pelle P. har förslagit en lösning, där man använder derivering för att få
fram det minsta värdet.
Han utnyttjar en kvadratisk plåt med sidan 11,7 dm
(avrundat värde).
Lådan har då avrundat måtten 5,85 x 5,85 x 2,92 (dm)
Den totala yttre arean blir då ≈ 102,60 dm2
|
 |
Alt. 1:
Lösning:
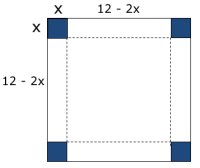
Klipp ut kvadrater i hörnen med sidan x dm och vik upp plåten.
Lådans volym: x(12 - 2x)2 = 100 (se figur)
Efter förenkling får man x3 - 12x2 + 36 x -25 = 0
Vi försöker gissa en rot till ekvationen och ser ganska lätt att x = 1 är en rot
till ekvationen.
Efter en polynomdivision får man en andragradsekvation, som ger ytterligare en
lösning:
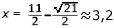 Lådans bottenyta har sidan 12 - 2 . 3,2 = 5,6 (dm)
Lådans bottenyta har sidan 12 - 2 . 3,2 = 5,6 (dm)
Det är den lösningen som redovisas i svaret. (x = 1 ger en låda med större vikt)
Alt. 2:
Bevis för att basytan är kvadratisk när den totala yttre arean är så liten som
möjligt
1) Enl. Pelle P.
Basytan i lådan är xy och höjden är z
V = xyz
A = xy + 2xz + 2 yz
z = V/xy  A = xy +
2V/y + 2V/x A = xy +
2V/y + 2V/x
Derivera först med avseende på x och sedan på y
A'(x) = y - 2V . x-2
A'(y) = x - 2V . y-2
Sätt båda derivatorna lika med 0
y - 2V . x-2 = 0
 x2y = 2V
(1) x2y = 2V
(1)
x - 2V . y-2 = 0
 xy2 = 2V
(2) (1) och (2) ger x = y dvs. kvadratisk botten xy2 = 2V
(2) (1) och (2) ger x = y dvs. kvadratisk botten
2)
Antag att basytan i lådan är en kvadrat med sidan x och att höjden är h (dm)
Vi jämför med att basytan är en rektangel med samma area, där sidorna är ax och bx.
Summan av faktorerna a och b är alltid > 2
när basytorna ska vara lika stora.
Ex:
Om a = 0,8 måste b = 1,25 0,8x . 1,25x = x2
0,8 + 1,25 = 2,05
Sammanlagda arean av de lodräta väggarna i lådan om basytan är en rektangel:
2 . 0,8xh + 2 . 1,25xh = 4,1xh
Sammanlagda arean av de lodräta väggarna i lådan om basytan är en kvadrat: 4xh Slutsats: Den totala arean är minst när basytan är kvadratisk.
Lösning:
Antag att basytan är x2 dm2
Då är höjden 100/x2 dm
f(x) är en funktion som beskriver den totala yttre arean
f(x) = x2 + 4x .
100/x2
f'(x) = 2x - 400x-2
f'(x) 0 =  2x - 400x-2
= 0 2x - 400x-2
= 0
x = 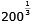 ≈ 5,85 dm ≈ 5,85 dm
Höjden är
 |
|