|
hur
gammal är tomten? |
Svar: Tomten är 75 år 2018
Lösning:
Tomten måste vara född på 1900-talet för att siffersumman av födelseåret ska
vara lika med hans ålder 1960.
Antag att tomten är född år 19xy
Hans ålder 1960 är då (1 + 9 + x + y) x < 6 och y
≤ 9
Ekv.: 1900 + 10x + y + (1 + 9 + x + y) = 1960
11x + 2y = 50
x = (50 - 2y)/11
x = 4 och y = 3
Tomten är alltså född 1943.
(Heltalslösningen x = 2 och y = 14 strider mot villkoret y
≤ 9)
År 2018 är tomten (2018 - 1943) år = 75 år.
|
 |
|
|
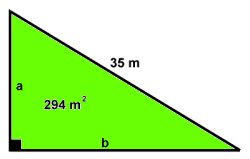
trädgårdslandet |
Svar: Staketet är 84 m
Lösning:
ab/2 = 294 (1) Triangelns area
a2 + b2 = 352 (2)
Pythagoras sats
2ab = 1176 (1)
a2 + b2 + 2ab = 352
+ 1176 (2)
(a + b)2 = 2401
(2)
a + b = ± 49
Endast det positiva värdet duger
Staketets längd: 49 m + 35 m = 84 m
|
 |
|
|
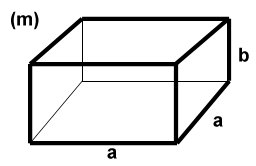
Poolen |
Svar: Polens mått är 4 x 4 x 2 m
Lösning:
Volym: a2b = 32
(1)
Total area: f(a) = a2 + 4ab
(2)
b = 32/a2
(1)
f(a) = a2 + 128/a (2)
f(a) = a2 + 128a-1
(2)
Derivera och sätt derivatan lika med 0
f '(a) = 2a -128a-2
2a -128a-2
= 0
a3
= 64
a = ± 4
Basytans mått är 4 x 4 m.
Då är höjden 32/42 m = 2 m |
 |
|
|
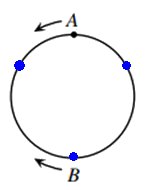
Skidträning |
Svar: Förhållandet är 2:1
Lösning:
Antag att Benjamin åker snabbast.
Eftersom de möts på samma tre punkter, måste dessa vara jämt fördelade på
slingan.
Till nästa möte måste Benjamin åka 2/3 av banan medan Adam åker 1/3 av banan.
Benjamin åker alltså dubbelt så fort som Adam.
Anm.: De blå punkterna är mötespunkter
|
 |
|
|
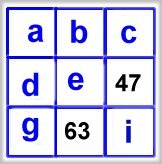
tomtens
magiska kvadrat |
Svar:
a) 55
b)
a = medelvärdet av 63 och 47.
Motsvarande samband gäller för talen i de andra hörnen.
Ex.: g = (b + d)/2
c)
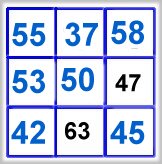
Se figur längst ner till höger.
Lösning:
a)
a + e = c + 47
a + d = 63 + i
Ledvis addition ger
2a + d + e = 110 + c + i
Men c+ i = d + e
2a = 110
a = 55b)
Bevis
c)
Summan av varje rad/kolumn/diagonal är tre gånger så stor som talet i
mittenrutan.
Summan = 3 . 50 = 150
Bevis
|
 |
|