|
slädfärden |
Svar: 10 km
Lösning:
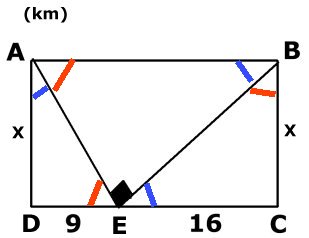
Trianglarna ADE, BCE och ABE är likformiga.
Vi jämför först trianglarna ADE och BCE.
x/16 = 9/x
x2 = 144
x = ± 12
Sträckorna AE och BE kan beräknas med Pytagoras sats eller likformighet.
AE = 15 och BE = 20
Omvägen är 15 km + 20 km - 25 km = 10 km längre. |
 |
|
|
jULKLAPPEN |
|
|
K |
L |
A |
P |
P |
|
+ |
K |
L |
A |
P |
P |
|
|
T |
O |
M |
T |
E |
T = 3
Vi inser då att K = 1.
Vi inser också att P = 6
(entals - och tiotalskolumnen)
Då är E = 2
Vi inser också att L ≥ 5, eftersom man får en minnessiffra i
tiotusentalskolumnen.
L = 5
Vi testar om L = 5.
M måste vara en udda siffra, 7 eller 9, eftersom vi har en minnessiffra
i hundratalskolumnen.
M kan inte vara 7, för då skulle A = 3.
Alltså är M = 9 och A = 4
Då blir O = 0
Vi har hittat en lösning!
En undersökning av övriga fall,
L = 7, 8 eller 9 ger ingen lösning. |
|
Svar: |
1 |
5 |
4 |
6 |
6 |
|
+ |
1 |
5 |
4 |
6 |
6 |
|
|
3 |
0 |
9 |
3 |
2 |
|
|
|
|
1 |
L |
A |
6 |
6 |
|
+ |
1 |
L |
A |
6 |
6 |
|
|
3 |
O |
M |
3 |
2 |
|
|
|
1 |
5 |
4 |
6 |
6 |
|
+ |
1 |
5 |
4 |
6 |
6 |
|
|
3 |
0 |
9 |
3 |
2 |
|
|
|
|
tomtesäcksloppet |
Svar:
a) Hela stafettloppet är 8 100 m.
b) Varje stafettlag består av nio tomtar.
Lösning:
Antag att hela stafettloppet är x m
| Tomte |
Sträckans längd (m) |
Återstår av loppet |
| Tomte nr 1 |
100 + (x - 100)/10 = 0,1x
+ 90 |
x - (100 + (x - 100)/10) =
0,9x - 90 |
| Tomte nr 2 |
200 + (0,9x - 90 - 200)/10
=
200 + 0,09x - 29 = 0,09x + 171 |
|
Alla tomtarna springer
lika lång sträcka
Ekv.: 0,1x + 90 = 0,09x + 171
0,01x = 81
x = 8100
En stafettsträcka är 0,1x + 90 = (0,1 . 8100 + 90) m = 900 m
Antal tomtar: 8100/900 = 9 |
|
|
|
träning inför tomtesäckloppet |
|
|
Svar: Kl. 10.20
är avståndet
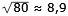 km. km.
Lösning:
Antag att tomtarna är närmast varandra x timmar efter kl. 10.00.
Alfred och Bertil har då hunnit till punkterna A och B.
Alfred har sprungit (10 + 10x) km och Bertil cyklat
20x km.
|
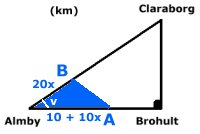 |
Cosinussatsen för den blå triangeln ger:
f(x) = (AB)2 = (20x)2 + (10 + 10x)2 - 2
. 20x(10 + 10x) . cos v
cos v = 20/25 = 4/5
Efter förenkling får vi
f(x) = 180x2 - 120x + 100
Vi deriverar och sätter derivatan lika med noll för att hitta ett minimivärde
f '(x) = 360x - 120
360x - 120 = 0
x = 1/3 1/3 h = 20 min
Avståndet är minst klockan 10.20
Avståndet är då
|
|