Månadens problem
december 2015 (lösning)

 

tomtesäcken
Svar: 66 julklappar
 

tomteverkstaden
Svar: Nisse tillverkade 36 godkända julklappar och 4 defekta julklappar (?)

Lösning:
Antag att Nisse tillverkade x godkända julklappar och y defekta julklappar.
 
Ekv.: 5x - 1,5y = 174
        50x - 15y = 1740  Denna diofantiska ekvation har många lösningar

Pelle Pels har skrivit den generella lösningen så här elegant:
x = 36 + 3n    n = 0, 1, 2, 3 .....
y = 4 + 10 n
           
Den första heltalslösningen blir x = 36 och y = 4
Nästa heltalslösning blir x = 39 och y = 14

Vi får nog anta att det inte är acceptabelt med en så stor andel defekta julklappar.
I så fall  hade Nisse nog inte fått jobba kvar i tomteverkstaden.
 

tomteslädarna del1

Svar:
a) Niklas kör med hastigheten km/h ≈ 26 km/h i en riktning som från väster avviker 30o mot norr.
b) Nisse och Niklas träffas efter 40 minuter.

Lösning:
Om Niklas ska färdas minsta möjliga sträcka, måsta hans färdriktning vara vinkelrät mot Nisses färdriktning.

 
Nisse startar i punkten A och Niklas i punkten B. De träffas i punkten C.
Vinklarna i triangeln ABC framgår av figuren.
Eftersom AB är 20 km, blir sträckan AC 10 km  och sträckan BC km
(Triangeln ABC är en halv liksidig triangel).
Med Nisses hastighet 15 km/h tar det 40 minuter att köra 10 km.
Under samma tid kör Niklas km. Hans hastighet måste då vara roten ur 3 gånger så stor som Nisses hastighet, dvs. km/h ≈ 26 km/h.
 

 tomteslädarna del2
Svar: Niklas ska hålla en kurs som från väster avviker 38,2o mot norr.

Lösning:


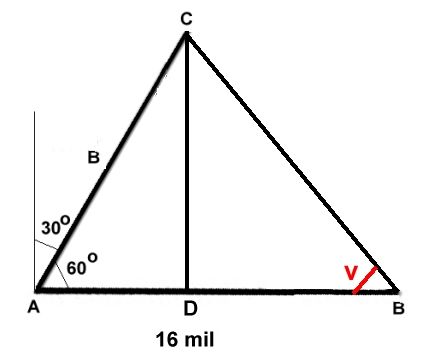
Antag att Nisse har kört x timmar och Niklas (x - 3) timmar när de möts.

Nisses hastighet är 20 km/h = 2 mil/h. Vinkeln CAD är 60o.
Sträckan AC är då 2x mil, sträckan AD x mil och sträckan DB (16 - x) mil.
Sträckan CD är x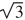 mil.
Sträckan BC är 7 (x - 3) mil 
Pytagoras sats på triangeln BCD ger (x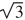)2 + (16 - x)2 = (7(x - 3))2
                                               3x2 + 256 - 32 x + x2 = 49x2 - 294x + 441
                                                   45x2 -262x +185 = 0

Lösningen av denna andragradsekvation
ger x1 = 5  (x2 = 37/45 förkastas, eftersom (x - 3) då är negativt)

Då är DB = (16 - 5) mil = 11 mil  och BC = 7(5 - 3) mil = 14 mil.
Beräkning av vinkeln v:
cos v = DB/BC = 11/14     v= arccos 11/14     v ≈ 38,2o
 

primtalen
Svar: Tomtefar tänkte på primtalen 2 och 3.

Lösning:

    y + x + 1 = xy
   x(y - 1) = y + 1
   x(y - 1) = (y - 1) + 2
            x = (y - 1)/(y - 1) + 2/(y - 1)
            x = 1 + 2/(y - 1)
Det finns två fall som ger heltalslösningar:
Fall 1:  y = 2 x = 3
Fall 2:  y = 3 x = 2

I båda fallen blir primtalen 2 och 3.
 

 slädfärden

Svar: Punkten B ligger ungefär 797 m från punkten A.
Genom att efter punkten B ta genvägen till D, blir tiden 277,6 s.
Tiden för att åka den plogade vägen AC-CD är 1800/6 s = 300 s
Tidsvinsten blir 22,4 s. Det är frågan om den lilla tidsvinsten motiverar att ta den besvärligare genvägen över sjön.
Lösning:
 Antag att sträckan BC är x m.
Då är sträckan AB = (1400 - x) m och sträckan BD = (x2 + 4002)1/2
Tiden för sträckan AB-BD blir  (1400  - x)/6 + (x2 + 4002)1/2/5
Vi kan behandla det här uttrycket som ett max- och minproblem, dvs. derivera uttrycket och sedan sätta derivatan lika med noll.
x ≈ 603
Sträckan AB 1400 m - 603 m = 797 m
Sträckan BD beräknar vi med Pytagoras sats till ungefär 723,6 m
Tiden blir 797/6 s + 723,6/5 s ≈ 277,6 s

 Tillbaka