|
i
tidningen |
|
Svar: På ett
tidningsuppslag har den vänstra sidan alltid ett jämnt nummer! |
|
Stockarna |
Svar: 153 stockar
Lösning:
Ovanför den mellersta raden finns det åtta rader. Då måste det
finnas åtta rader under den mellersta raden, dvs. sammanlagt 17 rader.
Det finns 18 stockar i rad 1 + rad 17, i rad 2 + rad 16, ... rad 8 + rad
10.
I raden i mitten finns det nio stockar.
Sammanlagt finns 8 . 18 + 9 = 153 stockar
Anm.: Detta är summan av en aritmetisk serie.
Summan kan beräknas med formeln
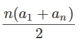
n = antalet termer, a1 = första termen och an =
sista termen |
|
|
Parkeringsplatsen |
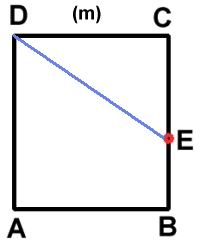
Svar: Parkeringsplatsen har måtten
5 m x 4 m
Lösning: Triangeln CDE är rätvinklig.
Det gäller alltså att undersöka om det finns en rätvinklig triangel där
de tre sidorna är tre på varandra följande naturliga tal.
Antag att CE är (n - 1) m, CD är n m och
DE är (n + 1) m.
Pytagoras sats ger (n - 1)2 + n2 = (n + 1)2
n2 - 2n + 1 + n2 = n2
+ 2n + 1
n2
- 4n = 0
n( n - 4) = 0
( n1 = 0 )
n2 = 4
Den egyptiska triangeln med sidorna 3, 4 och 5 är den enda rätvinkliga
triangel, där sidorna är tre på varandra följande positiva heltal.
CD = 4 m, CE = 3 m och BE = 2m, dvs. BC = 5 m. |
 |
|
|
matteboken |
Svar: 400 m
Lösning:
Antag att han vände om efter x km och att gånghastigheten
var a km/h
Hastigheten när han sprang var 150 % av a km/h = 1,5 a km/h
Ekv.:
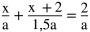
1,5x + x + 2 = 3
2,5x = 1
x = 0,4
0,4 km = 400 m
OBS! Svaret är oberoende av vilken hastighet han höll. Det är
bara hastighetsökningen när han sprang, som påverkar
resultatet. |
|
den kinesiske prinsen |
Svar: Placera en
svart pärla i den ena vasen och resten av pärlorna i den andra
vasen.
Lösning:
Sannolikheten att få upp en svart pärla från den första
vasen är naturligtvis 1 och sannolikheten att ta en svart pärla
från den andra vasen är 99/199.
Sedan måste vi också ta hänsyn till att sannolikheten för att
mandarinens dotter väljer en viss vas är 0,5.
Den sammanlagda sannolikheten för att mandarinens dotter tar upp
en svart pärla är
0,5 . 1 + 0,5 . 99/199
≈ 75 %
Anm.: Om de vita och svarta pärlorna varit jämnt
fördelade mellan vaserna hade sannolikheten varit
0,5 . 50/100 + 0,5 . 50/100
= 50 % |
|
risgrynsgröt och Mjölk
|
Svar:
a) 4 dl mjölk
b) 20 tomtenissar
Lösning:
a)
Antag att det från början var x tomtenissar som skulle få a
dl mjölk
I verkligheten var det (x - 5) tomtenissar som fick (a + 1) dl
mjölk
10 l = 100 dl
Ekvationssystem
x . a = 100
(1)
(x - 5)(a + 1) = 100 (2)
Ekv. (1) kan skrivas x = 100/a (3)
Efter förenkling blir ekv. (2) ax + x - 5a - 5 = 100 (4)
x = 100/a insatt i ekv. (4) ger efter förenkling
20 - a2 = a
Denna andragradsekvation har lösningen
a1 = 4
(a2 = - 5)
b) Enligt ekv. (3) blir x = 100/a = 100/4
x = 25
I verkligheten var det (x - 5) tomtenissar = (25 - 5)
tomtenissar =
20 tomtenissar, som åt gröt den kvällen. |
|