Problem för hängmattan
och badstranden del
2 del
2  |
|
7:an |
Svar: Det finns fyra
heltalslösningar
Lösning:
(a - 1) . (b +
2) = 7
Eftersom 7 är ett primtal, måste
parentesfaktorerna i vänsterledet
vara 1 och 7 eller -1 och -7.
|
a= 2 |
b = 5 |
|
a = 8
|
b = - 1 |
|
a = 0 |
b = - 9 |
|
a = - 6 |
b = - 3 |
|
|
|
|
avvänjningskliniken |
Svar: 7 patienter
behandlades för rökning och alkoholproblem.
Lösning:
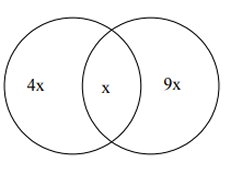
Låt x vara antalet
rökare som också är alkoholister bland alla patienter. De
utgör
20 % av rökarna. Antal rökare som inte är alkoholister är 80
% eller 4x.
x är också 10 % av alkoholisterna. Därför är antalet
alkoholister som inte är rökare 9x.
Ekv.: x + 4x + 9x = 98
x = 7
|
 |
|
|
ångbåten |
Svar: Motorbåtens kurs avviker från
väster mot norr med 38,2o.
Lösning:
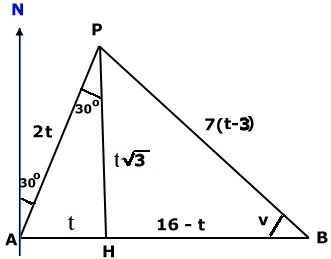
Motorbåten genskjuter ångbåten
i punkten P.
Antag att ångbåten kör sträckan AP på t timmar.
Avståndet AP är då 2t mil. Vinkeln APH är 30o
(alternatvinkel till vinkeln NAP).
Då är AH = AP/2 = t mil och
HP =
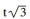
Avståndet HB = (16 - t) mil och avståndet BP
= (7(t - 3) mil.
Pythagoras sats på triangeln
HBP ger efter förenkling |
 |
45t2 -262t +185 = 0
t1 = 5
(t2 = 37/45)
Den andra roten till andragradsekvationen duger inte,
eftersom
t > 3 (enligt uppg.)
Motorbåtens kurs = vinkeln v
cos v = HB/BP = 11/14
v ≈ 38,2o
|
|
|
vägningen |
a) Svar: De fem
eleverna väger sammanlagt 303 kg
Lösning:
Eleverna är A, B, C, D och E.
A vägs till sammans med B, C, D och E. Det innebär att varje
elev vägs 4 gånger.
Eleverna väger sammanlagt
(129 + 125 + 124 + 123 + 122 + 121 + 120 + 118 + 116 +
114)/4 = 303
b) Svar: A: 65 kg, B:64 kg, C: 60 kg, D: 58 kg, E: 56
kg
Lösning:
Alla viktuppgifter är olika. Det innebär alla eleverna har
olika vikt.
Antag att A>B>C>D>E.
Då är A + B = 129, A + C = 125, E + D = 114 och E + C = 116
303 - 129 (dvs. A + B) - 114 (dvs. E + D) = C = 60 kg
Då är A = 125 - 60 = 65 kg och B = 64
kg. E = 116 - C = 116 - 60 = 56 kg
D = 114 - E = 58 kg
|
|
|
ett vinklat
problem |
Svar: Vinkeln EAC +
vinkeln ABC = 90o.
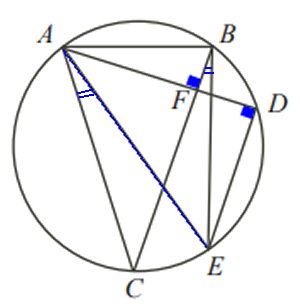
Lösning:
Sträckan DE är
parallell med sträckan BC.
Då är vinkeln D = 90o,
eftersom vinkeln F är 90o.
Eftersom randvinkeln D är 90o,
är AE diameter.
Då är även vinkeln EBA 90o.
Vinkeln EBC = vinkeln EAC (randvinklar på samma cirkelbåge)
Då gäller att EAC + ABC = EBC + ABC = EBA = 90o.
|
 |
|
|
punkten p |
a)
Bevis:
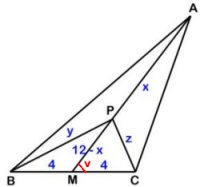
Medianen AM är 12 cm och
BM = CM = 4 cm.
Antag att AP = x cm, BP = y cm och
CP = z cm. Då är MP = (12 - x) cm.
0 ≤ x ≤ 12
Enligt mediansatsen i triangeln BPC är
2(BP)2 +
2(CP)2 = 4(MP)2 + (BC)2
2y2 + 2z2 = 4(12 - x)2
+ 82
y2 + z2 = 2(12 - x)2
+ 32
Addera med x2
i båda leden.
x2
+ y2 + z2 =
x2
+ 2(12 - x)2 + 32
Då ser vi att summan av de tre kvadraterna x2
+ y2 + z2 endast är
beroende av x, dvs. punkten P:s läge på medianen AM
V.S.B.
b)
Svar: För att summan av kvadraterna ska bli så liten som
möjligt, är AP = 8
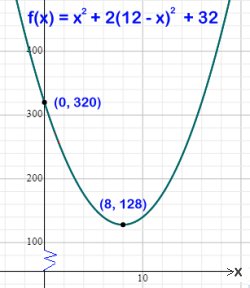
Se graf till höger.
x2
+ y2 + z2 är då 128
cm2
Lösning:
Problemet kan lösas med derivering
Låt f(x) = x2 + 2(12 - x)2 + 32
f(x) = 3x2
- 48x + 320 Derivera!
f ' (x) = 6x - 48
f ' (x) = 0 => 6x - 48 = 0 x = 8
Då är f(x) = 3 . 82 - 48
. 8 + 320 = 128
|
 |
|
c)
Svar:
Definitionsmängden är 0 ≤ x ≤ 12.
För att summan av kvadraterna (fx-värdet) ska bli så stor
som möjligt, är AP = 0
Se graf till höger.
x2
+ y2 + z2 är då 320
cm2
Lösning:
Grafen har en minimipunkt i (8, 128) enligt uppg. b)
Max-värdet för f(x) måste då ligga i ändpunkten 0 av
intervallet 0 ≤ x ≤ 12
eftersom ändpunkten 12 har ett lägre f(x)-värde.
Alltså är f(x)MAX
= 3x2
- 48x + 320 = 3 . 0 - 48 .
0 + 320 = 320 cm2
|
Pelle P. och Staffan R. har utnyttjat
cosinussatsen för att lösa
a-uppgiften:
Vinkeln CMP betecknas
med v, då
är BMP 180-v
Man har sambandet allmänt att
cos(v)
= -cos(180-v)
Cosinussatsen ger
y2 = 42
+ (12 - x)2
- 2 . 4(12 - x) .
cos(180-v)
z2 = 42
+ (12
- x)2
- 2
.
4(12 - x)
.
cos(v)
=>
y2 = 42
+ (12 - x)2
+ 2 . 4(12 - x) .
cos (v)
z2 = 42
+ (12
- x)2
- 2
.
4(12 - x)
.
cos(v)
=>
y2 + z2
= 32
+ 2
. (12 -x)2
Addera x2
i båda leden
x2 + y2 + z2
= x2 +32
+ 2
. (12 -x)2
Då ser vi att summan av de tre kvadraterna
x2
+ y2 + z2 endast är
beroende av x, dvs. punkten P:s läge på medianen AM
V.S.B. |

|





