Månadens problem
augusti 2020 (lösning)

 

Problem för hängmattan och badstranden   del 2     
a)
Svar: 17 passagerare
Lösning:
Vi kallar vagnarna A, B, C, D och E
I vagn A är antalet passagerare (p)  1 ≤  p ≤  5
Om p>5, uppfylls inte villkoret att varje passagerare har exakt 5 eller exakt 10 grannar.
Antalet passagerare i en vagn och dess angränsande vagnar är 6 eller 11.
Ex.:
      A            B              C              D             E
   2    4 5 2 4

 2 + 4 + 5 + 2 + 4 = 17

      A             B             C             D             E
   3    3 5 3 3

 3 + 3 + 5 + 3 + 3 = 17

17 passagerare gäller inte bara i de två exemplen ovan utan också när antalet passagerare i vagn A är 1, 4 eller 5.
b)
Svar: 5 passagerare
5 passagerare i den mellersta vagnen gäller inte bara i de två exemplen ovan utan också när antalet passagerare i vagn A är 1, 4 eller 5.
 Cadet 2016:24
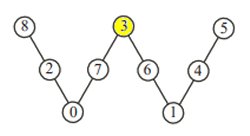
Uppg. 2:
Svar:  8991
Lösning:
Vi försöker hitta ett mönster

x

x2

Siffersumma (x2)

 9

81

9

99

9801

18

999

998001

27

9999

99980001

36

Siffersumman i talet x2 = 9 . antalet siffror i x
                                  9 . 999 = 8991
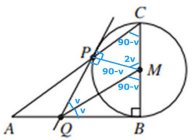
Uppg. 3:

Bevis:
Radien PM är vinkelrät mot tangenten PQ.
QB och QP är tangenter. Då är vinkeln BQM = vinkeln PQM. (beteckna dessa vinklar med v.)
Då är vinkeln BMQ = PMQ = 90 - v
Då är vinkeln PMC = 2v eftersom en rät linje är 180o.  (180 - (90 - v) - (90 - v) = 2v).
Triangeln CMP är likbent.
Då är vinkeln C = (180 - 2 v)/2 = 90 - v
Eftersom vinkeln BMQ = vinkeln BCA är QM parallell med AC
 
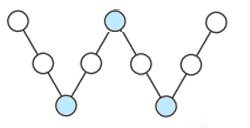
Uppg. 4:
Svar: 2015
Lösning:
Heltalen 2012-2020 ska placeras ut.
För att få enklare tal, ersätter jag heltalen 2012-2020 med heltalen 0-8.
Summan av heltalen 0-8 är 36 (som är delbar med 4).
Vart och ett av talen i de blå cirklarna till höger ingår i summan av två linjer. Summan av dessa tre tal måste då också vara delbar med 4. De tal, som bildar den minsta summan som är delbar med 4, är talen 0, 1 och 3.
Summan av de fyra linjernas tal blir
36 + 4 = 40. Varje linjes summa är därför
40/4 = 10.
Vi undersöker vilket av talen 0, 1 och 3 som passar in i den gula cirkeln.
Resultatet blir att talet 3 passar in.
(Om vi placerar 0 eller 1 i den gula rutan kommer en linje att innehålla talen 0 och 1. Då skulle det mellersta talet vara 9, vilket är omöjligt, eftersom det största talet är 8.)
Lösningen kan se ut som den nedersta figuren visar.
Talet 3 motsvarar det ursprungliga talet 2015.
 

 
Uppg. 5:
Svar: 1/3 a.e.
Lösning:
Eftersom DE, EF och DG är parallella med var sin sida i triangeln, får vi tre topptrianglar som är likformiga med triangeln ABC.
Antag att sträckan BD är kc    0<k<1
Då är BG ka och DG kb

 
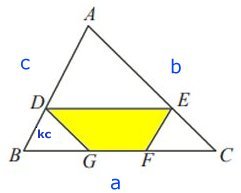
Likformighet (trianglarna BDG och ABC)
Arean av triangeln ABC är 1 a.e.
Förhållandet mellan sträckorna i trianglarna BDG och ABC är kc/c = k
Areaskalan = (längdskalan)2
Arean av triangeln BDG blir k2 a.e., eftersom arean av triangeln ABC är 1 a.e. Likformighet (trianglarna ADE och ABC)
Sträckan AD är c -kc = c(1 - k)
Förhållandet mellan sträckorna i trianglarna ADE och ABC är c(1 -k)/c = 1 -k
Då är förhållandet mellan areorna (1 - k)2.
Arean av triangeln ADE blir (1 - k2) a.e.
Likformighet (trianglarna CEF och ABC)
Eftersom AD är c(1 - k) är AE b(1 - k).
Då är CE = b - b(1 - k) = bk
Förhållandet mellan sträckorna i trianglarna CEF och ABC är kb/b = k
Då är förhållandet mellan areorna k2
Arean av triangeln CEF blir k2
Arean av parallelltrapetset DEFG = 1 - k2 -(1 - k)2 - k2 = 2k - 3k2
Arean f(k) = 2k - 3k2
Derivera för att få reda på maximala area.
f '(k) = 2 - 6 k   Sätt derivatan = 0
2 - 6k = 0
       k = 1/3
Maximala arean blir
Pelle P. har kommit fram till följande intressanta samband: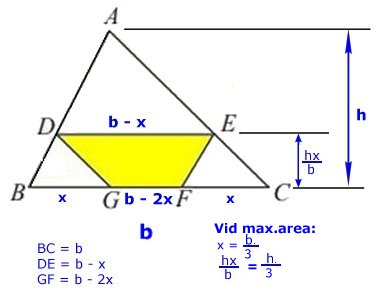

 

Tillbaka