|
Månadens
problem |
Problem för hängmattan
och badstranden |
|||
|
|||
|
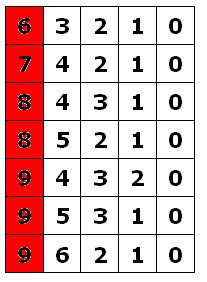
Uppg. 2: Svar: 168 tal Lösning: Villkoret att alla siffror ska vara olika, medför att den första siffran måste vara 6, 7, 8 eller 9 (i de röda rutorna). Den första siffran är lika med summan av de övriga siffrorna (i de vita rutorna ) i varje rad. De övriga siffrorna kan kastas om på 4! = 4 . 3 . 2 . 1 = 24 sätt. Tabellen till höger innehåller sju rader. Därför finns det 7 . 24 = 168 femsiffriga tal med de egenskaper som anges i uppgiften. |
 |
||
|
Uppg. 3: Svar: Sannolikheten för att åtminstone en ska klara examen är 91 % Lösning: Sannolikheten för att att inte klara examen är respektive 0,6 0,5 och 0,3 Sannolikheten för att ingen ska klara examen är 0,6 . 0,5 . 0,3 = 0,09 Sannolikheten för att åtminstone en ska klara examen är 1 - 0,09 = 0,91 =91 % |
|||
|
Uppg. 4: a) Svar: 29, 92, 38, 83, 47, 74, 56, 65 Lösning: Antag att man startar med talet 10x + y Talet med omkastade siffror är är då 10y + x Summan v de båda talen är (10x + y) + (10y + x) = 11(x + y) Eftersom detta tal är en jämn kvadrat och 11 är ett primtal, måste (x + y) = 11. Det gäller med andra ord att hitta de tal i intervallet 20 - 99, där summan av tiotalssiffran och entalssiffran är 11. |
|||
|
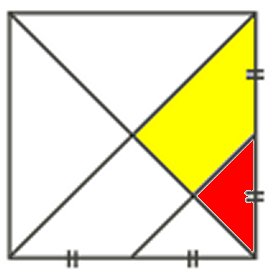
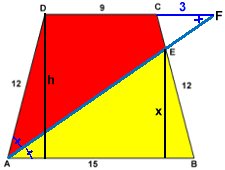
Uppg. 5: a) Svar: 23/25 Lösning: När sträckorna AE och DC förlängs, skär de varandra i punkten F. Man kan lätt visa att trianglarna ABE och CEF är likvinkliga och därmed likformiga. Det medför också att triangeln AFD är likbent. Då är sträckan CF = 12 cm - 9 cm = 3 cm. |
 |
||
|
Antag att höjden i
parallelltrapetset är h och höjden i triangeln ABE är x. Då är höjden i triangeln CEF h - x Likformighet för trianglarna ABE och CEF ger att x = 5h/6 Arean av parallelltrapetset är h(15 + 9)/2 = 12 h Arean av triangeln ABE är Arean av fyrhörningen ADCE är 12h - 25h/4 = 23h/4 Förhållandet mellan den röda och gula arean är 23/25 |
|||
|
|||