|
Månadens
problem |
Problem för hängmattan
och badstranden |
|||
|
Uppg. 1: Svar: 1:2 Lösning: Runt varje blå platta finns det sex vita plattor. Men samtidigt ser vi att den vita plattan markerad med x ingår i tre sådana konfigurationer. Förhållandet mellan blå och vita plattor är därför inte 1:6 utan 1:2. |
 |
||
|
Uppg. 2: Svar: A = 4, B = 7 och C = 2 Lösning: Värdet av talet ABC: 100A + 10B + C Värdet av BC: 10B + C Värdet av ABC - 2 . BC = 100A + 10B + C - 2(10B + C) 100A - (10B +C) 100A - (10B +C) = 328 A = 4 10B + C = 400 - 328 = 72 B = 7 c= 2 |
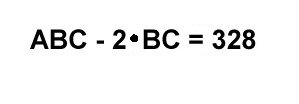 |
||
|
|||
|
Uppg. 4: a) Svar: x = 16 (16 + 9 = 25) a) Svar: y = 14 Lösning: Talet i den gula rutan är 17 (21 = 4 + 17) Vilka tal ska stå i den gröna och den blå rutan? Svar: Två tal som bildar summan 22. (22 = 2 + 20 går inte, eftersom 20 redan finns i översta raden). Talen är 10 och 12, men hur ska de placeras? Svar: 10 kan inte placeras i den blå rutan, eftersom siffrorna 8 (10 = 2 + 8) och 7 (10 = 3 + 7) redan är utplacerade. Alltså finns 10 i den gröna rutan och 12 i den blå rutan. Talet y måste vara 13 eller 14. Men 13 kan inte skrivas som summan av två grannar. Det kan däremot 14 (14 = 2 + 12)
|
|
||
|
Uppg. 5: Svar: 3/16 Lösning: G = Gary vinner D = David vinner Utgången av de två första omgångarna vet vi. Vi beräknar därför sannolikheten för de återstående omgångarna David kan vinna på följande sätt: GGDDDD Sannolikhet (D) = (1/2)4 = 1/16 Sannolikheten för utgången av var och en av de fyra sista omgångarna är 1/2 GGGDDDD Sannolikhet (D) = (1/2)5 = 1/32 Sannolikheten för utgången av var och en av de fem sista omgångarna är 1/2 GGDGDDD Sannolikhet (D) = (1/2)5 = 1/32 GGDDGDD Sannolikhet (D) = (1/2)5 = 1/32 GGDDDGD Sannolikhet (D) = (1/2)5 = 1/32 Sammanlagt: 1/16 + 4 . 1/32 = 3/16 |
|||


