|
Månadens
problem |
Problem för hängmattan
och badstranden |
|
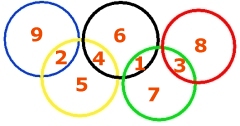
Uppgift 1: Lösning: Siffran 9 kan bara ligga i en av de yttersta cirklarna. Närmaste granne blir då siffran 2. Kan vi fortsätta med siffran 8? I så fall får 8:an även siffran 1 som granne och siffrorna 1, 2, 8 och 9 är då utplacerade. |
 |
|
Till de tre positionerna i den
gröna cirkeln kan man då välja mellan siffrorna 3, 4, 5, 6
och 7. Redan de tre minsta talen (3, 4 och 5) ger summan 12! Vi måste alltså hitta en annan placering av 8:an och prövar istället positionen längst till höger. 8:an får då siffran 3 som granne. Man ser genast att siffrorna 4, 5 och 6 inte kan placeras längst ner i den gröna cirkeln, eftersom den siffra som då ska skrivas i snittet mellan den svarta och gröna cirkeln redan är utplacerad. Då återstår att placera siffran 7 längst ner i den gröna cirkeln och sedan är det lätt att placera ut övriga siffror. jan 2014 |
|
|
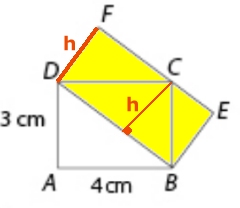
Uppgift 2: Svar: 12 cm2 Lösning: Arean av ABCD är 12 cm2. Arean av triangeln BCD är hälften så stor, 6 cm2. Eftersom triangeln BCD och rektangeln DBEF har samma bas och samma höjd är arean av rektangeln DBEF 12 cm2. nov 2011 |
 |
|
Uppgift 3: Svar: 20 sexhörningar Lösning: Det finns 12 femhörningar Varje femhörning gränsar till fem sexhörningar: 12 . 5 = 60 Men eftersom varje sexhörningar gränsar till tre femhörningar blir antalet sexhörningar 60/3 = 20 mars 2012 |
 |
|
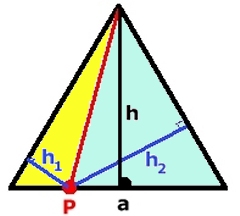
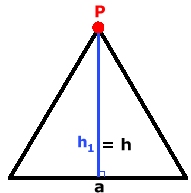
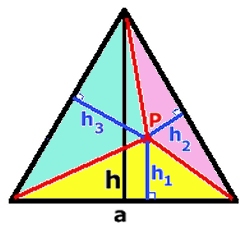
Uppgift 4: Lösning: Fall 1: Punkten P ligger inuti triangeln. Den liksidiga triangelns area: a.h/2 = a.h1/2 + a.h2/2 + a.h3/2 h = h1 + h2 + h3
|
|