Månadens problem augusti 2017

Månadens problem
augusti 2017

Problem för hängmattan och badstranden del 2

Uppgift 1: De olympiska ringarna Vid OS i Rio satt professor Kalkyl och ritade upp de olympiska ringarna. Inuti de fem cirklarna finns nio områden. Professor Kalkyl skrev in talen 1-9 i var sitt område. - Märkligt, muttrade professor Kalkyl, summan av talen i varje cirkel har blivit 11. Hur placerade professor Kalkyl de nio talen? Ledning
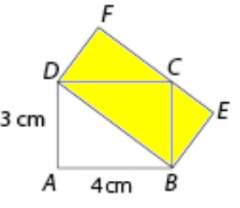
Uppgift 2: Rektanglarna ABCD och DBEF är rektanglar. Beräkna arean av rektangeln DBEF. En elev i åk 9 skulle kanske resonera så här: Sträckan DB kan jag beräkna med Pytagoras sats och sträckan DF kan jag räkna ut med hjälp av likformighet. Men det finns en enklare lösning som en duktig elev i åk 6 skulle kunna klara. Hur ser den lösningen ut?
Uppgift 3: The buckyball Vid VM 1970 användes en s.k. "buckyball" (uppkallad efter arkitekt Buckminster Fuller) med vita regelbundna hexagons (sexhörningar) och svarta pentagons (femhörningar) för att bollen skulle synas bra i TV. Varje femhörning gränsar till fem sexhörningar och varje sexhörning gränsar till tre femhörningar och tre sexhörningar. Det finns 12 femhörningar. Hur många sexhörningar finns det?
Anm.: Buckyball är också en kolmolekyl som består av 60 kolatomer. Den kemiska formeln är C₆₀. Tre forskare belönades med 1996 års nobelpris i kemi för upptäckten av C₆₀.
Uppgift 4: Den grymme sultanen När den grymme sultanens närmaste man, Abdullah, påstod att han var smartare än sultanen, blev han dömd till döden. Sultanen, som var övertygad om att han var smartast, sade: Du får en sista chans att klara dig. Om du i morgon kan visa att du är duktigare i geometri än vad jag är, ska du bli benådad. Abdullah funderade hela natten och när morgonen kom, hade han sin strategi klar. Han ritade upp en liksidig triangel med 6 m sida på sultanpalatsets gård. Sedan sade han: Jag påstår att även om Ers Nåd får välja att ställa sig först i den liksidiga triangeln, så kommer Ers nåd inte att hitta en punkt, där det sammanlagda avståndet till de tre sidorna är mindre än det sammanlagda avståndet är från den punkt, som jag kommer att välja.
Med ett självsäkert leende sade sultanen: Om inte mitt sammanlagda avstånd är mindre än ditt, blir du benådad. Annars kommer du att avrättas idag. Kunde verkligen Abdullah vara säker på att vinna?