Svar: Vinkeln v är 27,0
grader (och sträckan AB är 2,55 m.)
Lösning:
Antag att sträckan AB är x m.
Tiden för ångvälten att komma till punkten A blir
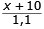 s
(t = s/v)
s
(t = s/v)
Sträckan AD blir enligt Pytagoras sats
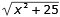 s
s
Tiden för myran att komma till punkten A blir då
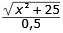 s
s
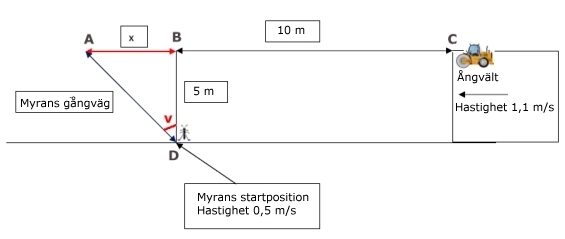
Tiden som funktion av x för skillnaden mellan ångvältens och
myrans tider blir
t(x) =
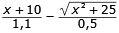
Detta max.problem kan vi lösa genom att sätta funktionens
derivata lika med 0.
t`(x) = 0 blir
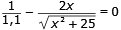
Den andra termen i vänstra ledet flyttas över till högra ledet.
Multiplicera båda leden med minsta gemensamma nämnaren och
kvadrera sedan båda leden.
Efter förenkling får vi 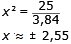
|
v
≈
arctan 2,55/5
v
≈
27,0
grader |
Om vi
ersätter x med 2,55 i funktionen t(x) får vi
tidsskillnaden till 0,18 s.
Med andra ord en väldigt snäv tidsmarginal även i det
mest optimala fallet.
Pelle Pels skriver: "Hade jag varit myra, hade jag
väntat tills ångvälten kört förbi. |
|
Anm.: Kan en myra verkligen
komma upp i så hög hastighet som 0,5 m/s?
Enligt zoologen Johan Lind har man faktiskt mätt upp hastigheten
0,5 m/s för en vandringsmyra i Sydamerikas regnskogar, men för
de flesta myror är hastigheten betydligt lägre, kanske 5 cm/s.
Myrfrågor (Sveriges Radio) |
|
|