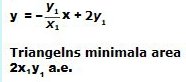|
|
a)
Svar: Pete Sampras
Lösning:
Om man vinner setet med 6-3 efter ett
servegenombrott, har man börjat
serva i setet.
Om vinnaren av setet istället
började som mottagare i setet, blir setsiffrorna 6-4 efter ett
servegenombrott.
b)
Svar: Servegenombrottet kom i sista gamet.
Lösning: Pete Sampras började serva i första set.
6-3 innebär sammanlagt nio game.
Då börjar Stefan Edberg serva i andra set. Om han börjar
serva och inte vinner med 6-3 utan bara med 6-4, måste servegenombrottet ha kommit
i sista gamet.
|
|
a)
Svar:
6 : 11
Lösning: Antag att det var x pojkar och y
flickor, när skidskolan startade.
Efter några veckor är det lika många pojkar och flickor,
(x+ 11) pojkar och (y - 13) flickor.
Ekvation: x + 11 = y - 13
x = y - 24
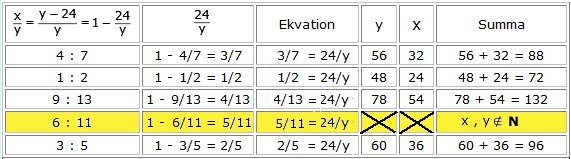
Förhållandet 6 : 11, när skidskolan startade, ger
inte heltalsvärden för antalet pojkar resp. flickor.
b)
Svar: Differensen mellan palindromtiderna är jämnt delbar
med 11.
Lösning:
Antag att första och sista siffran i segrarens tid var a
och att andra och tredje siffran var b samt att första
och sista siffran i tiden på 10:e plats var c och att
andra och tredje siffran var d.
Segrarens tid: 10a + b + 0,1b + 0,01a sekunder =
10,01a +
1,1b sekunder
Tiden på 10:e plats: 10,01c
+ 1,1d sekunder
Slutsats: Eftersom 10,01 och 1,1 är jämnt delbara med 11,
är differensen mellan "palindromtiderna" jämnt
delbar med 11.
|
|
|
|
Svar: Sannolikheten att
timern är inställd på mellan fyra och fem timmar är 7/20
Lösning:
Timern går på kl. 19.00, 19.30 eller 20.00
Om timern går på kl. 19.00, är den på mellan fyra och fem
timmar, om den går av mellan kl. 23.00 och 24.00. Sannolikheten
för att det sker är 1/2 (timern går ju av mellan kl. 23.00 och
01.00).
Sannolikheten
för att timern går på kl. 19.00 är 1/5. Dessa två villkor ger
sannolikheten
1/5 .
1/2
= 1/10.
Om timern går på kl. 19.30 eller kl. 20.00 gäller
ett liknande resonemang.
Timern går på kl. 20.30
Om timern går på kl. 20.30 är den på mellan 4 och fem timmar
mellan kl. 00.30 och 01.00. Det ger sannolikheten
1/5 .
0,5/2
= 1/20.
Timern går på kl. 21.00
Då kan inte timern vara på mer än fyra timmar.
Slutsats: Sannolikheten för att timern
är på mellan fyra och fem timmar är
3
.
1/10 + 1/20 =
7/20
|
|
|
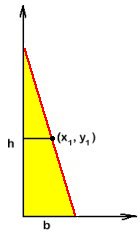
Svar: Linjens
ekvation är y = -2,5x +10 och triangelns
minmala area 20 a.e.
Lösning: |
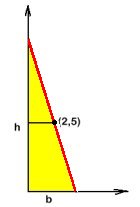
Vi ska bestämma
1) den röda linjens ekvation
2) den gula triangelns area, när den är så liten
som möjligt

Extrauppgift:
Svar:
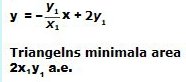
Lösning:
 |
|
|
|
|
|
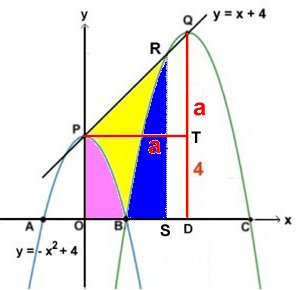
Svar: Punkten C har
koordinaterna (8,0)
Lösning:
Den blå grafen
Punkten P: x = 0. Då är y = 4,
eftersom y = - x2 + 4 P =
(0,4)
I punkterna A och B är y = 0, dvs.
x2 = 4 x = ± 2
A = (-2,0) och B = (2,0)
Den gröna grafen
Antag att Q har x-koordinaten a.
Då har Q y-koordinaten a + 4, eftersom
linjen genom Q har ekv.
y = x + 4
|
|
Grafens symmetrilinje har flyttats a steg åt höger. Då ska x
ersättas med (x - a) jfr med uppg. 5 nov21
Den gröna grafen har ekvationen
y = - (x - a)2 + 4 + a
y = - x2 + 2ax - a2 + 4 + a (1)
Grafen går genom punkten B = (2,0)
Sätt in (2,0) i ekvation (1)
0 = - 22 + 4a - a2 + 4 + a
a2 - 5a = 0
a(a - 5) = 0
a1 = 0 duger inte
a2 = 5
Då är BD = 5 - 2 = 3 = DC
Punkten C har koordinaterna (8,0) |
|
Extrauppgift:
1)
Svar:
Den gula arean är 28/3 a.e.
Lösning:
Beräkning av R:s koordinater
Den gröna grafen: y = - x2 + 10x -16
Linjen genom p och Q: y = x + 4
Ekvation: - x2 + 10x -16 = x + 4
x2 - 9x + 20 = 0
x1 = 5 dvs. Q har koordinaterna (5,9)
x2 = 4 dvs. R har koordinaterna (4,8)
Parallelltrapetset OPRS: 4(4+8)/2 = 24
Arean BOP (violett):
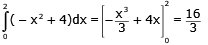
Arean BRS (blå):
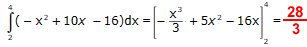
Den gula arean: 24 -16/3 - 28/3 =
28/3 (a.e.)
2)
Svar: De blå och gula areorna är exakt lika stora. |