|
|
Svar: Endast det
tresiffriga talet 625 uppfyller villkoret.
Staffan R.:s lösning:
Det tal som bildas av de två sista siffrorna måste ha
slutsiffran 1, 5 eller 6 och vara mindre än 32. Pröva
med 11, 21, 31, 15, 25 och 26. Endast 25 duger.
Kvadraten på 25 är 625. Enda talet är 625.
|
|
|
Svar:
Lösning:
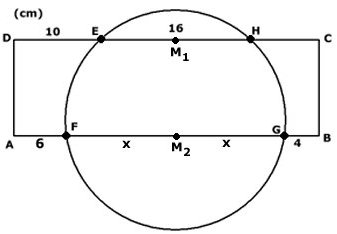
M1 är mittpunkt på sträckan EH och M2
är mittpunkt på sträckan FG.
FM2 = M2G = x (se figur)
Sträckan AM2 = DM1
Ekv.:
6 + x = 10 + 16/2
x = 12
Sträckan AB =
( 6 + 12 + 12 + 4) cm = 34 cm |
 |
|
|
Svar: 52 guldtackor
Lösning:
De 24 lättaste guldtackorna hade en genomsnittlig
vikt av 45/24 % = 1,875 % av den totala vikten.
De 13 tyngsta guldtackorna hade en genomsnittlig vikt av
26/13 % = 2 % av den totala vikten.
Övriga guldtackor har en genomsnittlig vikt (v) som
uppfyller villkoret
1,875 % < v < 2 % av den totala vikten.
Vikten av övriga guldtackor motsvarar 100 % - 45 % - 26
% = 29 % av den totala vikten.
Antalet övriga guldtackor
> 14 (Eftersom 29 %/14 > 2 %)
15: 29 %/15 ≈ 1,93 % Uppfyller villkoret
1,875 % < v < 2 %
16: 29 %/16 ≈ 1,81 % Uppfyller inte
villkoret 1,875 % < v < 2 %
Abdullah har 24 + 13 + 15 = 52 guldtackor
|
|
|
Svar: 1000 m
Lösning:
|
|
|
|
Problemet kan
lösas genom derivering, men det ger jobbiga
uträkningar.
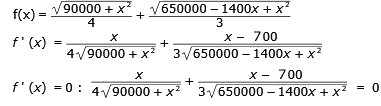
Kan det vara så att man valde enkla värden när
man konstruerade uppgiften?
Låt oss testa lite:
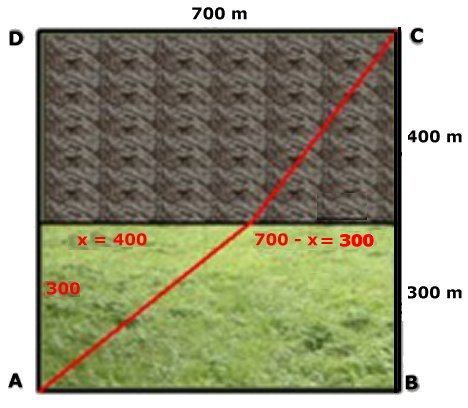
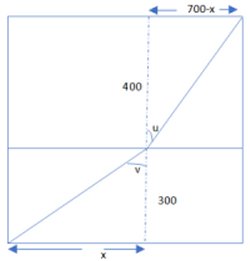
Eftersom hastigheten är högst på ängsmarken,
måste det vara gynnsammast om professor Kalkyl
når den plöjda marken till höger om diagonalen
AC.
Om han springer längs hypotenusan i en egyptisk
triangel både på ängen och
den plöjda marken, blir sträckan 500 m + 500 m =
1000 m. Kan det stämma?
I så fall är x = 400
Genom prövning eller genom derivering och
lösning av f '(x) = 0 online, finner vi att x =
400 är en lösning till f ' (x) = 0
Genom att studera f(x) inser man att x = 400 ger
en minimipunkt. |
|
Staffan R: har ett intressant
förslag till lösning:
För att
på kortaste tid ta sig fram måste Kalkyl
springa som om han vore en ljusstråle i
de två medierna.
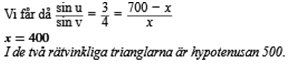
Han skulle alltså springa 1000 m på
291,67 s.
Om han skulle springa diagonalt, skulle
sträckan bli 989,95 m och tiden 294,63
s.
Tiden y för professor Kalkyl blir
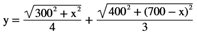
Man kan visa, efter jobbig derivering,
att y har ett minimum
för x = 400 |
 |
|
|
|