Månadens problem
april 2019 (lösning)

terrängloppet
Svar: Bo vann och Doris kom sist
Lösning:
 
Påståenden:
Doris blev nummer 5 och Anne nummer 3.                 
Bo blev nummer 2 och Erik nummer 3.                      
Erik blev nummer 1 och Carina nummer 4.                 
Anne blev nummer 2 och Doris nummer 1.                 
Carina blev nummer 4 och Bo blev nummer 2.            
 
(1)
(2)
(3)
(4)
(5)


Vi får först göra ett antagande och se om det stämmer, t.ex. att Bo inte kom tvåa.
Då är Erik nummer 3 enligt (2) och Carina nummer 4 enligt (5)
Då kan Anne inte vara nummer 3. Därför blir Doris nummer 5 enligt (1)
Då är Anne nummer 2 enligt (4). Nu återstår bara plats nummer 1 och den tar Bo.
 

Det mystiska sambandet

Svar: Problemet kallas Collatz förmodan.
Det verkar som om man alltid till slut hamnar på talet 1, men det har man som sagt inte kunnat bevisa.
Anm. 1: För att till slut hamna på 1, måste man tidigare ha hamnat på talet 2n
n = 1, 2, 3....
Ännu har alltså ingen lyckats bevisa att man alltid hamnar på 2n vilket positivt tal man än börjar på.
Anm. 2: Det finns inget direkt samband mellan talets storlek och antalet steg i lösningen.  Om man startar på talet 25 innehåller lösningen 23 steg, talet 26 10 steg och talet 27 111 steg!

Hypotenusan
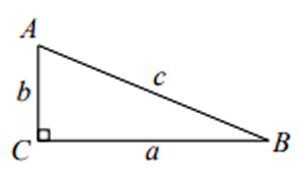
Svar: Hypotenusan är 65 cm
 
Lösning:
ab/2 = 504           
a + b + c = 144     
ab = 1008              
c = 144 - (a + b)    
 
(1)
(2)
(3)
(4)


Pythagoras sats ger
a2 + b2 = (144 - a - b)2
a2 + b2 = 1442 + a2  + b2 + 2ab - 288a - 288b
men ab = 1008 enligt (3)
Efter förenkling får vi
0 = 1442 + 2016 - 288(a + b)     Div. med 288
a + b = 72 + 7
a + b = 79
c = 144 - (a + b) = 144 - 79 = 65
 

Bollarna
Svar: Till slut är det en gul boll/gula bollar kvar.
Lösning:
Det finns så många varianter av lösningar, så det gäller att hitta ett allmängiltigt bevis.
Vi kan se att det från början är udda antal gröna och röda bollar och ett jämnt antal gula bollar.
Varje gång man tar bort två olikfärgade bollar och lägger dit en boll av den tredje färgen sker en förändring för alla tre färgerna när det gäller egenskapen udda/jämn.
Antalet gröna och röda bollar måste därför alltid ha samma egenskap när det gäller udda/jämn medan det för antalet gula bollar är tvärtom.
När proceduren till slut leder till att två färger försvinner, måste det det vara grön och röd som försvinner, eftersom det är de två färgerna som samtidigt kan komma ner till noll bollar.
Anm:
Varje gång proceduren genomförs, minskar totala antalet bollar med en boll. Därför upprepas proceduren högst 11 gånger.
 

        Tillbaka