|
|
I ett terränglopp startar
Anne, Bo, Carina, Doris och Erik.
När de kommer hem, påstår de följande:
Doris blev nummer 5 och Anne nummer 3.
Bo blev nummer 2 och Erik nummer 3.
Erik blev nummer 1 och Carina nummer 4.
Anne blev nummer 2 och Doris nummer 1.
Carina blev nummer 4 och Bo blev nummer 2.
Kan det här verkligen stämma? Nej naturligtvis inte. |
(1)(2)(3)(4)(5) |
|
 |
I vart och ett av de fem
påståendena är en upplysning korrekt och en felaktig.
Vem vann och vem kom sist?
|
|
|
|
|
|
|
a) |
Välj slumpmässigt ett
positivt heltal. Om talet är jämnt ska du dela det med
2, men om talet är ojämnt ska du multiplicera det med 3
och sedan lägga till 1. Upprepa denna process med det
nya talet.
Vilket tal kommer du till slut att hamna på, om du
fortsätter på det sättet? |
|
b) |
Gör om beräkningarna med
några andra tal. Får du alltid samma svar? |
Anm. 1: Ingen
matematiker har lyckats bevisa om man alltid får samma
svar. En av 1900-talets stora matematiker,
ungraren Paul Erdős, sa:
Mathematics is not yet ready for such problems.
|
|
|
|
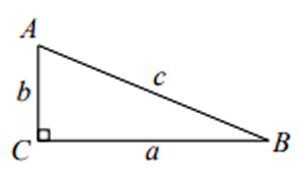
I
den rätvinkliga triangeln ABC är omkretsen 144
cm och arean 504 cm2.
Bestäm vilka värden hypotenusan c kan
anta. |
 |
|
|
|
Tre gröna, fyra gula och fem
röda bollar ligger i en påse.
Två bollar med olika färg tas bort slumpmässigt.
De ersätts med en boll av den tredje färgen.
(Det finns tillräckligt med extrabollar i reserv för att
kunna göra så).
Proceduren upprepas till dess att det bara finns en boll
kvar i påsen, alternativt att alla bollarna i påsen har
samma färg.
Vilken färg har bollen/bollarna då?
|
 |