Svar: Diametern i den
mellersta cirkeln är 24 cm
Lösning:
Trianglarna OAP, OBQ och OCR är likformiga
(topptriangelsatsen)
Då är även de likbenta trianglarna APZ, BQX och CRY likformiga.
Dessutom är trianglarna AXP och BYQ likformiga och sträckorna AX
och BY parallella.
r1/r2 = AO/BO = XO/YO = BO/CO (trianglarna
OBX och OCY)
Men BO/CO = r2/r3
Alltså är r1/r2 = r2/r3
På motsvarande sätt kan man visa att r1/r2
= r2/r3 = r3/r4
= r4/r5
Vi bildar nu ett ekvationssystem
r1/r2 = r4/r5
r2/r3 = r3/r4
r1r5 = r2r4
r2r4
= (r3)2
Eftersom båda ekvationerna innehåller r2r4
inser vi att r1r5 = (r3)2
Men vi vet ju att r1 = 18/2 cm = 9 cm och r5
= 32/2 cm = 16 cm
Alltså är (r3)2 = 9 . 16
(r3)2 = 144
r3 = ± 12 (Eftersom det gäller en sträcka, duger inte
det negativa värdet)
Staffan Rösby har skickat in följande lösning:
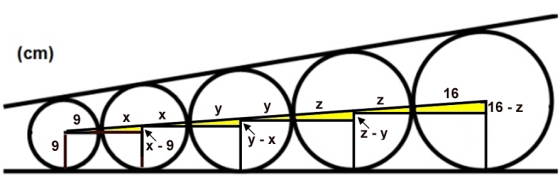
De fem cirklarnas medelpunkter och tangeringspunkter sammanbinds
med en rät linje.
En radie i varje cirkel dras mot den gemensamma
tangeringslinjen. Fyra rätvinkliga och likformiga trianglar
skapas.
De lodräta kateterna är i tur och ordning x - 9, y - x, z -y och
16 -z
 |