|
Geometri = problemlösning! |
Lätt:
Lösning:
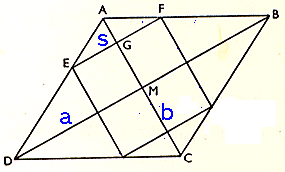
Δ AEF
~
Δ
ADB
Likformighet ger
(b/2 - s/2)/b/2 = s/a
(b - s)/b = s/a
ab - as = bs
ab = bs + as
Dividera med abs
1/s = 1/a + 1/b V.S.B. |
 |
Medel:
Svar: AB:BR = 3
Lösning:
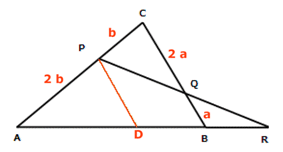
AP = 2b PC = b
CQ = 2a QB = a
Konstruktion: DP //BC
Antag att BR = x och AB = kx
Δ ADP
~
Δ
ABC
Likformighet ger
AP/AC = DP/BC
2b/3b = DP/3a
DP = 2a
Av samma skäl är AD = 2kx/3.
Då är DB = kx - 2kx/3 = kx/3
Δ RQB
~
Δ
RPD
BR/DR = BQ/DP
x/(kx/3 + x) = a/2a
6x = kx +3x
kx = 3x
k
= 3 |
 |
Svår:
Lösning:
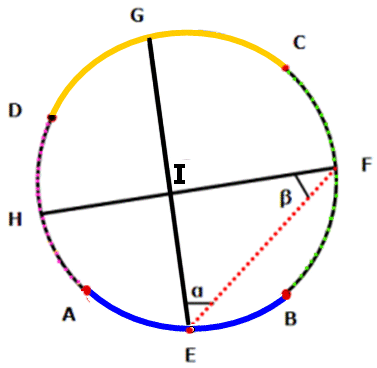
Låt vinkeln FEG = α
och vinkeln EFH = β
α är periferivinkel på bågen FG och β är periferivinkel på
bågen EH.
Av färgerna på cirkelns periferi framgår det cirkelbågarna
FG och EH är halva cirkelns omkrets. Då är summan av
motsvarande medelpunktsvinklar 180o
Eftersom periferivinkeln är hälften så stor som
medelpunktsvinkeln är
α + β = 90o
Studera triangeln EFI.
α + β = 90o
Då är vinkeln EIF =
180o - 90o =
90o
V.S.B. |
 |