Geometri = problemlösning!
|
Lätt:
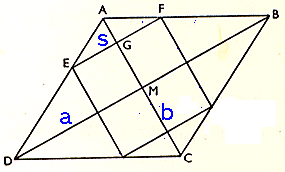
Diagonalerna i en romb är a och b. Den i romben inskrivna
kvadraten har sidan s. Bevisa att 1/a + 1/b =1/s
(Studentexamen för latinlinjen ht 1942) |
 |
Medel:
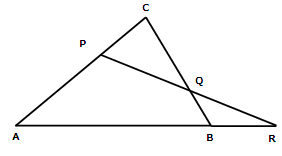
På sidorna AC och BC i triangeln ABC ligger punkterna P och
Q.
AP:PC=CQ:QB=2.
Linjerna AB och PQ skär varandra i R. Beräkna förhållandet
AB:BR.
(Lärobok från 60-talet för realgymnasiet åk 1 ) |
 |
Svår:
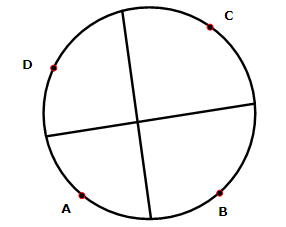
Låt A, B, C och D vara punkter på en cirkels
periferi, så att man får cirkelbågarna AB, BC, CD och DA.
Mittpunkten på bågen AB sammanbinds med mittpunkten på bågen
CD och mittpunkten på BC sammanbinds med mittpunkten på DA.
Visa att de erhållna sträckorna är vinkelräta mot varandra.
(Skolornas matematiktävling 14/10 1971). |
 |
|