Tänker du fel i hastigheten?
Lätt: En kuggfråga Det sista kugghjulet roterar lika snabbt som det första.
Medel: Medelhastighet Svar: Medelhastigheten blir 24 km/h. Lösning: Medelhastigheten blir inte (20 + 30) km/h = 25 km/h! Resan till Nässjö tar 1 h. Resan tillbaka till Eksjö tar 20/30 h = 2/3 h Hela restiden är därför 1 h + 2/3 h = 5/3 h. Resans längd ToR är 40 km. Hastigheten blir 40/(5/3) km/h = 24 km/h
Svår: Svar: Hanna måste öka sin hastighet med 37,5 % Lösning: När Amanda har hunnit 24 km, har Hanna cyklat 18 km. (Jämför med problemet "Annas ålder" http://mathpuzzle.se/svar3.htm) Amanda: Återstående sträcka: 40 km - 24  km = 16 km Hastighet: v km/h Tid: 16/v h Hanna: Återstående sträcka: 40 km - 18  km = 22 km Hastighet: xv km/h (där x är förändringsfaktorn) Tid: 22/xv h Hannas tid är samma som Amandas, eftersom de ska komma samtidigt till Mariannelund.   Ekv.:  16/v  = 22/xv xv/v = 22/16 x = 1,375 dvs. Hannas hastighet ökade med 37,5 %.
Ännu lite svårare: Svar: 200 m, 210 m och 290 m Lösning: Antag att de joggar i x h. 700 m =0,7 km Ekv.: 6,9 x + 7,1x = 0,7 x = 0,05
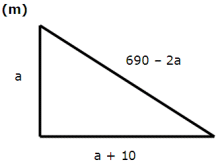
Den långsammare har därför joggat 6,9 . 0,05 km = 0,345 km = 345 m Den snabbare har joggat 7,1 .  0,05 km = 0,355 km = 355 m Eftersom de möts mitt på hypotenusan, kan vi dra slutsatsen att den ena kateten är 10 m längre än den andra kateten Antag att kateterna är a m resp. (a + 10) m. Hypotenusan blir då (700 - a - a - 10) m = (690 - 2a) Pythagoras sats ger: a2 + (a + 10)2 = (690 - 2a)2 Efter förenkling av andragradsekvationen får man (a1=  1190 duger inte)    a2= 200 Den mindre kateten är 200 m Den större kateten är (200 + 10) m = 210 m Hypotenusan är (700 - 200 - 210) m = 290 m