| 1 | 2 | 3 | 4 |
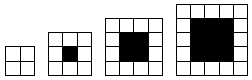
a) Figur nr 5:16 svarta rutor
b) Figur nr n: (n-1)2 svarta rutor
Klurigt nr 6 (lösningar)
Kolorna
| Svar: 20 kolor Ekvation: Första dagen: x kolor Andra dagen: 1,25x kolor Tredje dagen: 1,2*1,25 x kolor = 1,5x kolor x + 1,25x + 1,5 x = 75 x = 20 |
Torghandel
| Svar: Nej! Första krukan Ordinarie pris: 100/0,8 dirham = 125 dirham Förlust: 25 dirham Andra krukan Ordinarie pris: 100/1,25 dirham = 80 dirham Vinst: 20 dirham |
Mönster
Hur är följande mönster
uppbyggt?
a) Figur nr 5:16 svarta rutor |
Den här uppgiften innebär inte något lyft!
T. ex.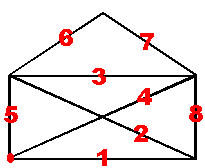 |
Den här uppgiften tillhör den moderna gren av
matematiken, som kallas topologi. Det kanske mest berömda exemplet är "Broarna i Königsberg (Kaliningrad)", som löstes av Euler långt innan topologin betraktades som en gren av matematiken. Lösning: Om ett udda antal kanter möts i ett hörn, kallas detta hörn udda. Problemet går att lösa endast om antalet udda hörn är 0 eller 2. I figuren till vänster är de två nedersta hörnen udda. Du måste starta i ett av dessa hörn. |
Sista stickan förlorar
| Resonera
"baklänges": Om jag lämnar kvar 5 stickor, kommer jag nästa gång att kunna lämna kvar 1 sticka oberoende av datorns senaste val. Med liknande resonemang kommer man fram till att det gäller att lämna kvar 9, 13, 17, 21 och 25 stickor. Oddsen är därför mycket goda! Endast när det från början finns 17, 21 eller 25 stickor vinner datorn, om jag spelar rätt. Eftersom datorn slumpmässigt väljer 14 - 28 stickor (= 15 möjliga fall), betyder det att jag har 80% chans att vinna. |
Vandraren och herdarna
| Svar: Den
ene herden fick 10,5 drachmer och den andre 1,5 drachmer. Beräkning: Sammanlagt 8 bröd. Var och en åt 8/3 bröd. Vandraren fick (5 - 8/3) bröd=7/3 bröd av den ene herden och (3 - 8/3) bröd=1/3 bröd av den andre herden. 12 drachmer skall alltså delas mellan herdarna i förhållandet 7:1. 12/8=1,5 7*1,5=10,5 |
Hur gamla var barnen?
| Svar: Barnen
var 9, 2 och 2 år. Beräkning: Efter den första ledtråden finns det många alternativ att välja mellan:
När det efter andra ledtråden inte går att avgöra barnens ålder, trots att man vet den sammanlagda åldern, måste det betyda att minst två alternativ ger denna summa. Av tabellen ovan framgår att summan är 13. Ledtråden "Mitt äldsta barn är blont" utesluter alternativet 1, 6 och 6 år. |
Tennismatchen
| Serveordning: Efter
första gamet skall mottagaren bli servare och servaren mottagare osv.
omväxlande i alla följande game av matchen. Vid ett servegenombrott i ett set gäller: Om den som servar i första gamet i ett set gör servegenombrottet, kan setsiffrorna bli 6 - 3 eller 6 - 4. Om den som är mottagare i första gamet i ett set gör servegenombrottet blir setsiffrorna 6 - 4. a) Eftersom första set gick till tiebreak, återstod (31 - 13) game = 18 game. Två set med sammanlagt 18 game och ett servegenombrott i vardera setet betyder att de båda seten slutade 6 - 3. För att serveordningen skall stämma, måste Sandra ha vunnit första set. Svar: Sandra vann med 7 - 6, 3 - 6, 6 - 3. b) Nej! Med totalt 32 game slutade ett av seten 6 - 4. Vid ett sådant resultat går det inte att avgöra vem som har gjort servegenombrottet! Setsiffrorna för matchen Sandra - Åsa kunde vara 7 - 6, 3 - 6, 4 - 6 eller 7 - 6, 3 - 6, 6 - 4 eller 7 - 6, 4 - 6, 3 - 6 eller 6 - 7, 6 - 4, 3 - 6. Anm.: Resonemanget ovan förutsätter att serveordningen har varit korrekt hela tiden. I regelhäftet (regel 15) står det "Om ett game avslutas innan misstaget (dvs. fel servare min anm.) upptäcks, skall serveordningen kvarstå ändrad. SvTFs kommentar: Att serveordningen kvarstår ändrad innebär att den spelare, som rätteligen skulle ha servat i gamet, i stället servar i nästa game och att serveordningen är ändrad också i återstoden av matchen jämfört med vad ursprungligen bestämts. |
Tomtesäcken
|
Säcken skall rymma 810 liter. (Tomtenissarna är 9, 9 och 10 år gamla.) Kommentar: Det här problemet kan nog duktiga låg- och mellanstadieelever lösa: Med hjälp av miniräknare kan man lätt testa olika värden och konstatera, att tomtenissarna bör vara så nära varandra i ålder som möjligt. Matematiskt kan man visa det genom derivering: 1) Antag, att tomtenissarna är x, y och (28-x-y) år 2) Tomtesäckens volym blir då xy(28-x-y)= 28xy-x2y-xy2 3) Derivering med avseende på x ger 28y-2xy-y2 4) Derivering med avseende på y ger 28x-x2-2xy 5) Sätt derivatorna lika med noll. 6) Efter förenkling får man 28-2x-y=0 och 28-x-2y=0 7) Bilda ett ekvationssystem av dessa ekvationer. 8) Lösningen till ekvationssystemet blir att alla tre tomtenissarna är 9 1/3 år. Eftersom alla fyller år den dagen duger bara heltalslösningar. Åldrarna 9, 9 och 10 år ger maximal storlek på säcken. Man kan även få fram lösningen med ett enkelt BASIC-program 5 REM Tomtenissarna är x1, y1 och z1 år. Säcken skall rymma r1 liter 10 R=0:R1=0 20 FOR X=1 TO 26 30 FOR Y=1 TO 26 40 FOR Z=1 TO 26 50 IF X+Y+Z=28 THEN GOSUB 200 60 NEXT Z 70 NEXT Y 80 NEXT X 90 CLS: PRINT:PRINT "Tomtenissarna är"X1;",";Y1;"och";Z1;"år" 100 PRINT "Säcken skall rymma";R1;"liter." 110 END 200 R=X*Y*Z 210 IF R>R1 THEN LET R1=R:X1=X:Y1=Y:Z1=Z 220 RETURN |
|
|