Klurigt nr 31 (lösningar)

Fotbollscupen   Tranås har vunnit sina tre matcher  och Vetlanda har förlorat sina tre matcher. Tranås måste ha vunnit med resultaten 2 - 1, 1 - 0 och 1 - 0. P.g.a. Nässjös och Vetlandas målskillnad inser vi att Tranås vann med 1 - 0 mot både Nässjö och Vetlanda. Det betyder att Tranås vann över Eksjö med 2 - 1. Lag Poäng Målskillnad Tranås 9 4 - 1 Eksjö 4 4 - 2 Nässjö 4 1 - 1 Vetlanda 0 0 - 5 Nässjö måste ha vunnit över Vetlanda med 1 - 0. Nässjö har också spelat en oavgjord match. Eftersom Nässjös målskillnad var 1 - 1, måste matchen Nässjö - Eksjö ha slutat 0 - 0. Eftersom Vetlanda förlorade mot både Tranås och Nässjö med 1 - 0, måste matchen Eksjö - Vetlanda ha slutat 3 - 0. Resultat: Tranås - Eksjö 2 - 1 Tranås - Nässjö 1 - 0 Tranås - Vetlanda 1 - 0 Nässjö - Eksjö 0 - 0 Nässjö - Vetlanda 1 - 0 Eksjö - Vetlanda 3 - 0
Bläckplumparna
Svar: 8 7 5 2 6 6 0 8 Lösning: Bartholomeus måste ha fått ett svar som ligger mellan 87 000 000 och 87 999 999. Vi antar det det mellersta av de tre talen är x. Ett bra närmevärde för x får vi om vi beräknar och . Det innebär att det mellersta (jämna) talet måste vara 444. 442 . 444 . 446 = 87 526 608
Den kinesiska asken
Svar: 64 cm3 Lösning: Antag att längd, bredd och höjd minskar med x, y resp. z cm. Kubens kanter blir då 40 - 4x = 28 - 4y = 20 - 4z   Dividera samtliga termer med 4! 10 - x = 7 - y = 5 - z Vi kan då dra slutsatsen att 1 ≤ z ≤ 4 Det innebär, att vi måste undersöka om kubens kant är (20 - 4.1) cm = 16 cm           V = 163 = (24)3 = 212  cm3 (20 - 4.2) cm = 12 cm           V = 123 = (22 . 3)3 = 26 . 33  cm3 (20 - 4.3) cm = 8 cm           V = 83 = (23)3 = 29  cm3 (20 - 4.4) cm = 4 cm           V = 43 = (22)3 = 26  cm3 =  64 cm3 Volymen för den största asken är 40 . 28 . 20 = 26 . 350 cm3 Vi ser då direkt att den största askens volym är endast delbar med volymen av den kub, som har kanten 4 cm! Denna kub har volymen 64 cm3.
Bilresan
Svar: 122 km Lösning: På de första skyltarna finns det två siffror, XY. Eftersom x är tiotalssiffra, är värdet av den siffran 10x. Då är avståndet på de första skyltarna 10x + y. På skyltarna i fig. 2 är avståndet till Huskvarna 100y + x (y är hundratals siffra) och till Linköping 10 y +x. Avståndet mellan Huskvarna och Linköping ger ekvationen 10x + y + 10 x + y = 100y + x + 10 y + x             20 x + 2y = 2x + 110y                      18x = 108 y                         x = 6y Eftersom x är ett ensiffrigt tal ≠ 0, inser man att y = 1. Då är x = 6 . 1 = 6 Avståndet är 61 km + 61 km = 122 km                      fig. 1                       fig. 2
Upp-och nervända världen
Svar: Dupond och Dupont hade vänt papperslappen upp och ner.
Dupond och matematiken
Svar: Triangeln hade sidorna 6, 8 och 10 l.e.          eller 5, 12 och 13 l.e. Lösning:
Kvadraten
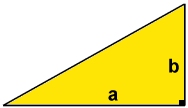
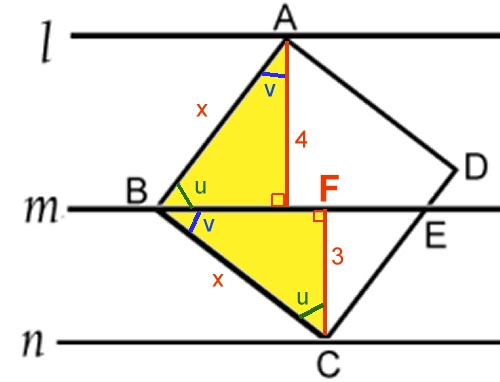
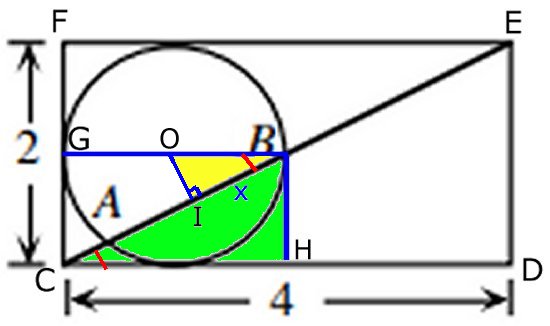
Svar: a) Kvadratens sida är 5 cm b) Sträckan BE är 6,25 cm Lösning: a) De båda gula trianglarna har lika stora vinklar. De är därför likformiga. Men eftersom de har lika stora hypotenusor ( = kvadratens sida) är de kongruenta. De båda gula trianglarna har därför kateterna 3 cm och 4 cm. Pytagoras sats ger att hypotenusan (kvadratens sida) är 5 cm. b) Triangeln BCE är likformig med triangeln BCF. Likformighet ger BE/BC = BC/BF    BE/5 = 5/4   BE = 25/4    BE = 6,25
Latinsk stötesten
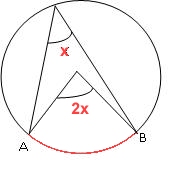
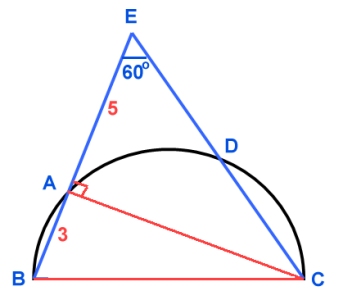
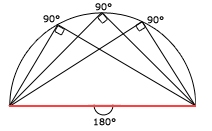
Svar: a) Sträckan DE är 4 cm b) Diametern är cm ≈ 9,2 cm Lösning: a) Genom likformighet kan man visa att DE . CE = AE . BE 10 . DE = 5  . 8       DE = 4 b) CE = 10 cm och AE = 5 cm Därför är triangeln ACE är en halv liksidig triangel  med 90 gradersvinkeln vid hörnet A. Enligt randvinkelsatsen är randvinkeln hälften så stor som medelpunktsvinkeln på samma cirkelbåge. (se fig. nedan) När randvinkeln är 90 grader, är cirkelbågen därför en halvcirkel. Då kan vi dra slutsatsen att BC är diameter i cirkeln! Höjden AC i den halva liksidiga triangeln ACE är cm Pytagoras sats på triangeln ABC ger 32 + ()2 = (BC)2 BC = ±
Något i hästväg?
Svar: Två hästar, 11 kor och 23 hönor Lösning: Ett primtal är ett heltal större än 1 som bara är delbart med 1 och sig självt: 2, 3, 5, 7 , 11, 13 ,17, 19, 23, 29 .... Antag att det fanns x hästar, y kor och z hönor. Ekvation y(x + y) = 120 + z (1) Låt oss undersöka följande alternativ: 1) x ≠ 2 y ≠ 2     Då är y(x + y) ett jämnt tal. I så fall är 120 + z ett jämnt tal. Enda möjligheten     är då att z = 2. Men svaret i högra ledet (122) kan bara delas upp som 2 . 61      (eftersom båda faktorerna måste vara större än 1).     Då är y = 2, men det dels strider antagandet att y ≠ 2 och dels att     x, y och z är olika primtal. 2) y = 2     Då är y(x + y) ett jämnt tal. I så fall är 120 + z ett jämnt tal. Enda möjligheten     är då att z = 2. Det duger inte eftersom x, y och z är olika primtal. 3) x = 2     Då är y(x + y) ett udda tal     Ekvation (1) kan då skrivas y(2 + y) = 120 + z                                          y2 + 2y - 120 = z        Beräkna nollställen till V. L.:    y2 + 2y - 120 = 0 ger  y1 = 10 och y2 = - 12     dvs. ( y - 10)(y + 12) = z     Eftersom z är ett primtal måste den första parentesen vara lika med 1 och den     andra parentesen vara lika med z.     Då är y = 11 och z = 11 + 12 = 23
Kordan Svar: Kordan AB är cm ≈ 1,8 cm Lösning: Drag sträckan BG parallell med rektangelns långsidor och BH parallell med rektangelns kortsidor. Antag att BG är diameter i cirkeln. I så fall är BG = CH = 2 cm och BH = 1 cm Med de angivna måtten är förhållandet mellan sidorna i triangeln BCH och triangeln CDE 1:2, dvs. trianglarna är likformiga och vi har därmed visat att BG är diameter i cirkeln. Vinkeln OBI = vinkeln BCH (alternatvinklar). Då är den gula triangeln och gröna triangeln likformiga. Antag att sträckan AB är 2x cm. Då är sträckan BI x cm. Likformighet ger BI/CH = OB/BC    BC beräknas med Pythagoras sats till cm. x/2 =       x =      2x =

|Tillbaka|