Svar: 300 kycklingar.
Lösning:
Antag att det finns n kycklingar och att fodret då räcker i x dagar.
Antag att dagsportionen för en kyckling är a kg
Mängden kycklingfoder kan då skrivas på tre olika sätt.
1) n.x.a kg
2) (n - 75).(x + 20).a kg
3) (n + 100).(x -15).a kg
Då kan vi ställa upp följande ekvationer
n.x.a = (n - 75).(x + 20).a
n.x.a = (n + 100).(x -15).a
Efter förenkling får vi
4n - 15x -300 = 0
-3n + 20x - 300 = 0
n = 300
Svar: Grönsakshandlaren hade åtminstone 946 apelsiner.
Lösning:
Antag att antalet apelsiner är x.
(x - 1) är jämnt delbart med 3, 5, 7 och 9.
Då är (x - 1) en multipel av 5 . 7 . 9 = 315 (Eftersom 9 är en multipel av 3, behöver vi inte ta hänsyn till trean.)
Därför gäller det att hitta ett värde på n, så att 315n + 1 är delbart med 11.
n = 1 315 + 1 = 316 duger inte!
n = 2 315 . 2 + 1 = 631 duger inte
n = 3 315 . 3 + 1 = 946 duger! (946/11 = 86)
Andra n-värden som duger är 14, 25, 36 .... (Kan du se något mönster?)
Svar: 28 elever har iPhone
Lösning:
Eftersom var och en av eleverna säger: "Jag har en Samsung men den elev som du senast intervjuade har en iPhone", måste detta innebära att varannan elev har en Samsung. (Om två Samsungägare eller två iPhoneägare kom efter varandra, skulle den andra av dessa säga: Jag har en Samsung och den elev som du senast intervjuade har också en Samsung.)
Vi vet inte om den första eleven talar sanning eller ljuger. Därför måste vi undersöka båda alternativen.
Alternativ 1:
Antag att den första eleven talade sanning.
Då vet vi att det var ett jämnt antal elever i bussen och att alla elever med udda nummer hade en Samsungtelefon.
Den längsta eleven och den som utfrågas fyra elever senare måste då båda vara iPhoneägare och tala osanning (annars skulle de ha gett samma svar). Samma sak gäller för den snyggaste eleven den som utfrågas sex elever senare.
Sammanfattning: Vi vet nu att svaren 19, 24, 26 och 13 inte stämmer.
Av den långhårigaste eleven och den som utfrågas fem elever senare är den ene Samsungägare (=sanningssägare) och den andre iPhoneägare (=lögnare). Men vi vet redan att svaret 13 är lögn. Det korrekta svaret är alltså 28.
Alternativ 2:
Antag att den första eleven talade osanning.
Med samma resonemang som ovan kommer vi fram till samma svar.
Svar: Ja, det går alltid att göra en rättvis fördelning oavsett hur många rum det finns i byggnaden..
Lösning:
Vi gör följande antaganden:
Antal rum: n
Antal kistor: n . n = n2
Antal mynt: n2 . n = n3
Befälhavaren för livvakten får en kista med guldmynt, dvs. n st guldmynt.
Då återstår det n3 -n guldmynt
n3 -n kan skrivas n(n2 -1) = n(n + 1)(n - 1) enligt konjugatregeln
Vi kastar om ordningen på faktorerna
n(n + 1)(n - 1) = (n - 1) . n . (n + 1)
Faktorerna i detta utryck består av tre på varandra följande heltal.
Då vet vi säkert att ett av talen är delbart med 3 och att minst ett av talen är delbart med 2. Ett tal som är delbart med både 2 och 3 är delbart med 6!
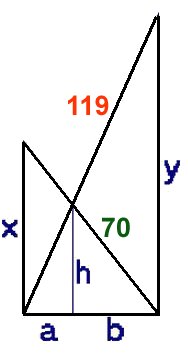
Svar: 56 m
Lösning:
Se figurens beteckningar.
Den sökta sträckan (bergsklyftans bredd) är (a + b) m.
Vi ersätter sträckorna a + b med beteckningen w
På grund av likformighet får vi
x/w = h/b (1)
y/w = h/a (2)
Ekvation (1) kan skrivas b = wh/x
Ekvation (2) kan skrivas a = wh/y
Bergsklyftans bredd är då w = wh/x + wh/y
1 = h/x + h/y
xy = hy + hx
y = hx/(x -h) (3)
Nu ska vi tillämpa Pytagoras sats på de trianglar där stegarna är hypotenusor.
w2 + x2 = 702
w2 + y2 = 1192
Om vi löser detta ekvationssystem får vi
y2 - x2 = 1192 - 702
y2 - x2 = 9261 (4)
Enligt ekv. (3) är y =hx/(x -h).
Vi vet också att h = 30 m
Ekv. (4) kan då skrivas
(30x/(x -30))2 - x2 = 9261
Detta ger en fjärdegradsekvation.
Enklast är väl att ta ett kalkylprogram till hjälp för att hitta rätt lösning.
x = 42 m
Med Pytagoras sats får vi
w2 + 422 = 702
w2 = 3136
w = ± 56